题目内容
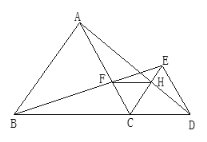
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
(1)求证:△BCE≌△ACD;
(2)求证:FC=HC
(3)求证:FH∥BD.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)先根据△ABC和△CDE都是等边三角形得出BC=AC,CE=CD,∠BCA=∠ECD=60°,再由SAS定理即可得出△BCE≌△ACD;
(2)由△BCE ≌ △ACD,可得∠CBF=∠CAH,然后根据“ASA”证明△BCF≌△ACH即可;
(3)根据∠FCH=60°,可知△CHF为等边三角形,进而可得出结论.
(1)∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴在△BCE和△ACD中,
BC=AC∠BCE=∠ACDCE=CD,
∴△BCE ≌ △ACD(SAS).
(2)∵△BCE ≌ △ACD,
∴∠CBF=∠CAH,
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上,
∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF,
在△BCF和△ACH中,
∠CBE=∠CAHBC=AC∠BCF=∠ACH,
∴△BCF≌△ACH(ASA),
∴CF=CH,
(3)∵∠FCH=60°,
∴△CHF为等边三角形
∴∠FHC=∠HCD=60°,
∴FH∥BD.

【题目】(1)下表是2008年北京奥运会部分国家金牌榜:
国家 | 中国 | 美国 | 俄罗斯 | 英国 | 德国 | 澳大利亚 | 本届奥运会金牌总数 |
金牌数 | 51 | 36 | 23 | 19 | 16 | 14 | 302 |
①选择 统计图来描述上表中各国金牌数最恰当.请把这个统计图画出来.
②请你根据统计图,写出两条与29届奥运会金牌数有关的信息.
(2)下表是中国奥运代表团自1984年第23届洛杉矶奥运会以来,历届奥运会的金牌总数统计表:
年份 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
届别 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
金牌数 | 15 | 5 | 16 | 16 | 28 | 32 | 51 |
①选择 统计图来描述上表中我国各届金牌数最恰当.把这个统计图画出来.
②请你根据统计图,写出两条与中国奥运金牌数相关的信息.