��Ŀ����
����Ŀ��2017��5�£�������Ŀ����һ��һ·�����ʺ����߷���̳�ڱ������У�Ϊ����ѧ������̵��˽���һ�ջ�������й����٣�ijУ��֯���꼶�װ���Ұ��ѧ����չ��һ��һ·��֪ʶ��������ֳ�����ʱ���װ���Ұ�ֱ�ѡ5��ͬѧ�μӱ������ɼ���ͼ��ʾ��

��1��������ͼ�������������±���
ƽ���� | ��λ�� | ���� | ���� | |
�װ� | 8.5 | 8.5 | _____ | _____ |
�Ұ� | 8.5 | ______ | 10 | 1.6 |
��2������Ϊ�ĸ���ijɼ��Ϻã�Ϊʲô��
���𰸡�88.50.7
��������
��1��������ͼ�ֱ�ó��ס��Ұ�5λͬѧ�ijɼ����ٸ�����������λ���ͷ�������ɵã�
��2���ֱ��ƽ��������������λ���ͷ���ĽǶȷ����ɵã�
��1���װ�5λͬѧ�ijɼ��ֱ�Ϊ8.5��7.5��8��8.5��10��
��װ�5λͬѧ�ɼ�������Ϊ8.5������Ϊ![]() ��[��8.5-8.5��2��2+��7.5-8.5��2+��8-8.5��2+��10-8.5��2]=0.7��
��[��8.5-8.5��2��2+��7.5-8.5��2+��8-8.5��2+��10-8.5��2]=0.7��
�Ұ�5λͬѧ�ijɼ��ֱ�Ϊ��7��10��10��7.5��8��
���Ұ�5λͬѧ�ɼ�����λ��Ϊ8��
��ȫ�������£�
ƽ���� | ��λ�� | ���� | ���� | |
�װ� | 8.5 | 8.5 | 8.5 | 0.7 |
�Ұ� | 8.5 | 8 | 10 | 1.6 |
��2����ƽ���������ס��Ұ�ɼ�һ����
����λ�������װ�ɼ��ã�
�����������Ұ�ɼ��ã�
�ӷ�����װ�ɼ��ȶ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�����ճ������У��۲���ֽ�����ĵذ壬���ܷ��ֵذ峣�ø���������ε�ש������������ͼ����Ҳ����˵��ʹ�ø�����ijЩ������Σ��ܹ�ƴ��һ��ƽ��ͼ�Σ��Ȳ�����һ˿�հף��ֲ������ص����ڼ��������ƽ����Ƕ��������Ȼ��������ε��ڽǴ�С�йأ���Χ��һ��ƴ��һ��ļ�������ε��ڽǼ���һ��ǡ�����һ���ܽǣ�360����ʱ����ƴ����һ��ƽ��ͼ�Σ�
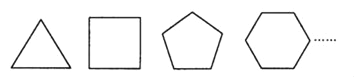
��1�����������ͼ�Σ���д���пո�
�������� | 3 | 4 | 5 | 6 | �� |
�������ÿ���ڽǵĶ��� | �� |
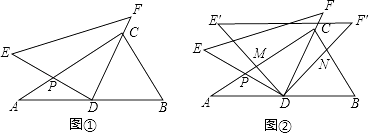
��2����ͼ�����������һ�����������Ƕ���ļ��������������Ƕ��һ��ƽ��ͼ�Σ�
��3���������Ρ����ı��Ρ�����������ѡһ�֣������������������ѡһ�֣��뻭���������ֲ�ͬ�����������Ƕ�ɵ�һ��ƽ��ͼ�Σ���ͼ������̽��������������ι�����Ƕ�ɼ��ֲ�ͬ��ƽ��ͼ�Σ�˵��������ɣ�
����Ŀ��ijУ���꼶ѧ����չ����ӱ������ÿ����5��ͬѧ�μӣ��������ֶܷ����������Σ��ڹ涨ʱ����ÿ����100������(��100)Ϊ���㣬�±��dzɼ���õļװ���Ұ�5��ѧ���ı�������(��λ����)��
1�� | 2�� | 3�� | 4�� | 5�� | �ܷ� | |
�װ� | 100 | 98 | 110 | 89 | 103 | 500 |
�Ұ� | 89 | 100 | 95 | 119 | 97 | 500 |
ͳ�Ʒ��������ܷ���ȣ���ʱ��ͬѧ���飬����ͨ�����������е�������Ϣ��Ϊ�ο����������������⣺
(1)��������������ʣ�
(2)������������ݵ���λ����
(3)��������������ݵķ�����һ��С��
(4)��������������Ϣ������ΪӦ�ðѹھ���״������һ���ࣿ�������ɣ�