题目内容
【题目】已知在△ABC中,AD⊥BC,垂足为点D,DE∥AC交AB于E,DF∥AB交AC于F,当△ABC再添加一个条件:时,四边形AEDF为菱形(填写一个条件即可).
【答案】AD平分∠BAC或AB=AC
【解析】解:若AD平分∠BAC,四边形AEDF是菱形, 理由:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴∠DAF=∠EAD,
∵∠EAD=∠DAF,
∴∠FAD=∠FDA,
∴AF=DF.
∴平行四边形AEDF为菱形.
若AB=AC,∵AD⊥BC,
∴DA平分∠BAC,四边形AEDF是菱形.
所以答案是:平分∠BAC或AB=AC.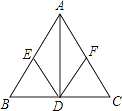
【考点精析】本题主要考查了菱形的判定方法的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.

练习册系列答案
相关题目
【题目】2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示:

(1)根据上图将计算结果填入下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | _____ | _____ |
乙班 | 8.5 | ______ | 10 | 1.6 |
(2)你认为哪个班的成绩较好?为什么?