题目内容
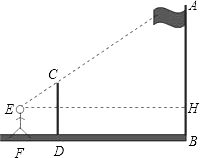
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过点C. 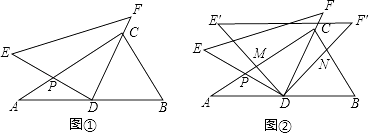
(1)求∠ADE的度数;
(2)如图②,在图①的基础上将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,求证: ![]() .
.
【答案】
(1)解:∵∠ACB=90°,点D为AB的中点,
∴CD=AD=BD= ![]() AB,
AB,
∴∠ACD=∠A=30°,
∴∠ADC=180°﹣30°×2=120°,
∴∠ADE=∠ADC﹣∠EDF=120°﹣90°=30°

(2)解:∵∠EDF=90°,
∴∠PDM+∠E′DF=∠CDN+∠E′DF=90°,
∴∠PDM=∠CDN,
∵∠B=60°,BD=CD,
∴△BCD是等边三角形,
∴∠BCD=60°,
∵∠CPD=∠A+∠ADE=30°+30°=60°,
∴∠CPD=∠BCD,
在△DPM和△DCN中,
![]() ,
,
∴△DPM∽△DCN,
∴ ![]() .
.
【解析】(1)首先证明∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC﹣∠EDF计算即可得解;(2)只要证明△DPM和△DCN相似,再根据相似三角形对应边成比例即可证明.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示:

(1)根据上图将计算结果填入下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | _____ | _____ |
乙班 | 8.5 | ______ | 10 | 1.6 |
(2)你认为哪个班的成绩较好?为什么?
【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 |
| 2 |
| … |
乙复印店收费(元) | 0.6 |
| 2.4 |
| … |
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.