ЬтФПФкШн
ЁОЬтФПЁПвбжЊAЁЂBЁЂCШ§ЕуВЛдкЭЌвЛжБЯпЩЯ.
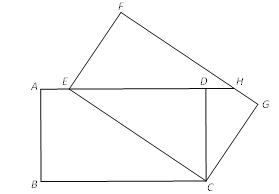
ЃЈ1ЃЉШєЕуAЁЂBЁЂCОљдкАыОЖЮЊRЕФЁбOЩЯЃЌ
ЂйШчЭМЂйЃЌЕБЁЯA=135ЁуЃЌR=1ЪБЃЌЧѓЁЯBOCЕФЖШЪ§КЭBCЕФГЄЃЎ
ЂкШчЭМЂкЃЌЕБЁЯAЮЊШёНЧЪБЃЌЧѓжЄЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЖЈГЄЯпЖЮBCЕФСНИіЖЫЕуЗжБ№дкЁЯMANЕФСНБпAMЁЂANЃЈBЁЂCОљгыAВЛжиКЯЃЉЛЌЖЏЃЌШчЭМЂлЃЌЕБЁЯMAN=60ЁуЃЌBC=2ЪБЃЌЗжБ№зїBPЁЭAMЃЌCPЁЭANЃЌНЛЕуЮЊPЃЌЪдЬНЫїдкећИіЛЌЖЏЙ§ГЬжаЃЌPЁЂAСНЕуМфЕФОрРыЪЧЗёБЃГжВЛБфЃПЧыЫЕУїРэгЩЃЎ
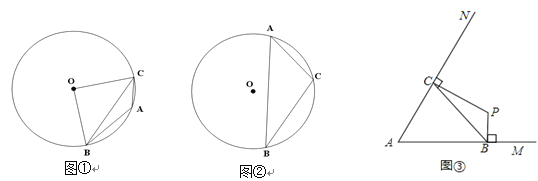
ЁОД№АИЁПЃЈ1ЃЉЂйЁЯBOC=90ЁуЃЌBC=![]() ЃЌЂкжЄУїМћНтЮіЃЛЃЈ2ЃЉдкећИіЛЌЖЏЙ§ГЬжаЃЌPЁЂAСНЕуМфЕФОрРыЪЧЗёБЃГжВЛБфЃЌРэгЩМћНтЮіЃЎ
ЃЌЂкжЄУїМћНтЮіЃЛЃЈ2ЃЉдкећИіЛЌЖЏЙ§ГЬжаЃЌPЁЂAСНЕуМфЕФОрРыЪЧЗёБЃГжВЛБфЃЌРэгЩМћНтЮіЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйИљОнЭЌЛЁЫљЖдЕФдВжмНЧЪЧдВаФНЧЕФвЛАыЃЌвђЮЊЁЯA=135ЁуЃЌЫљвдгХЛЁЫљЖдЕФНЧЁЯBOC=270ЁуЃЌЫљвдСгЛЁBCЫљЖдЕФЁЯBOC=90ЁуЃЌдйгЩЙДЙЩЖЈРэМЦЫуГіBCЕФГЄЖШЃЛЂкбгГЄCOНЛ![]() OгкЕуEЃЌСЌНгBEЃЌЫљвдЁЯA=ЁЯEЃЌвђЮЊCEЮЊ
OгкЕуEЃЌСЌНгBEЃЌЫљвдЁЯA=ЁЯEЃЌвђЮЊCEЮЊ![]() 0ЕФжБОЖЃЌЕУГіЁЯCBE=90ЁуЃЌЫљвдsinA=sinE=
0ЕФжБОЖЃЌЕУГіЁЯCBE=90ЁуЃЌЫљвдsinA=sinE=![]() =
=![]() ЃЛЃЈ2ЃЉСЌНгAPЃЌШЁAPЕФжаЕуKЃЌЗжБ№СЌНгCKЁЂBKЃЌгЩгкBPЁЭAMЃЌCPЁЭANЃЌзїKHЁЭBCНЛBCгкЕуHЃЌИљОнжБНЧШ§НЧаЮЮвУЧаББпЩЯЕФжаЯпЕШгкаББпЕФвЛАыЃЌЕУCK=BK=AK=PKЃЌМДЕуAЁЂBЁЂPЁЂCдквдKЮЊдВаФЃЌ
ЃЛЃЈ2ЃЉСЌНгAPЃЌШЁAPЕФжаЕуKЃЌЗжБ№СЌНгCKЁЂBKЃЌгЩгкBPЁЭAMЃЌCPЁЭANЃЌзїKHЁЭBCНЛBCгкЕуHЃЌИљОнжБНЧШ§НЧаЮЮвУЧаББпЩЯЕФжаЯпЕШгкаББпЕФвЛАыЃЌЕУCK=BK=AK=PKЃЌМДЕуAЁЂBЁЂPЁЂCдквдKЮЊдВаФЃЌ ![]() APЮЊАыОЖЕФдВЩЯЃЌЕБЖЈГЄЯпЖЮBCЕФСНИіЖЫЕуЗжБ№дкЁЯMANЕФСНБпAMЁЂANЃЈBЁЂCОљгыAВЛжиКЯЃЉЛЌЖЏЃЌШчЭМЃЌЕБЁЯMAN=60ЪБЃЌЁЯBKC=120ЃЌBC=2ЃЌМДЁїBKCЪЧвЛИіЖЅНЧЮЊ120ЁуЃЌЕзБпBC=2ЕФЕШбќШ§НЧаЮЃЌВЛФбЧѓГіCK=BK=
APЮЊАыОЖЕФдВЩЯЃЌЕБЖЈГЄЯпЖЮBCЕФСНИіЖЫЕуЗжБ№дкЁЯMANЕФСНБпAMЁЂANЃЈBЁЂCОљгыAВЛжиКЯЃЉЛЌЖЏЃЌШчЭМЃЌЕБЁЯMAN=60ЪБЃЌЁЯBKC=120ЃЌBC=2ЃЌМДЁїBKCЪЧвЛИіЖЅНЧЮЊ120ЁуЃЌЕзБпBC=2ЕФЕШбќШ§НЧаЮЃЌВЛФбЧѓГіCK=BK=![]() AP=
AP=![]() ЃЌМДAP=
ЃЌМДAP=![]() ЃЌЫљвддкећИіЛЌЖЏЙ§ГЬжаЃЌPЁЂAСНЕуМфЕФОрРыБЃГжВЛБфЃЎ
ЃЌЫљвддкећИіЛЌЖЏЙ§ГЬжаЃЌPЁЂAСНЕуМфЕФОрРыБЃГжВЛБфЃЎ
ЪдЬтНтЮіЃК
НтЃЈ1ЃЉЂйИљОнЭЌЛЁЫљЖдЕФдВжмНЧЪЧдВаФНЧЕФвЛАыЃЌЁпЁЯA=135ЁуЃЌ
ЁргХЛЁЫљЖдЕФНЧЁЯBOC=270ЁуЃЌ
ЁрСгЛЁBCЫљЖдЕФЁЯBOC=90ЁуЃЛ
дкRtЁїBOCжаЃЌгЩЙДЙЩЖЈРэПЩжЊBC=![]() =
=![]() .
.
Ђк
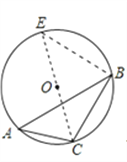
жЄУїЃКШчЭМЫљЪОЃЌбгГЄCOНЛ![]() OгкЕуEЃЌСЌНгBEЃЌ
OгкЕуEЃЌСЌНгBEЃЌ
ЁрЁЯA=ЁЯEЃЌ
ЁпCEЮЊ![]() 0ЕФжБОЖЃЌ
0ЕФжБОЖЃЌ
ЁрЁЯCBE=90ЁуЃЌ
ЁрsinA=sinE=![]() =
=![]() .
.
ЃЈ2ЃЉ
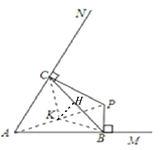
СЌНгAPЃЌШЁAPЕФжаЕуKЃЌЗжБ№СЌНгCKЁЂBKЃЌзїKHЁЭBCНЛBCгкЕуHЃЌ
ЁпBPЁЭAMЃЌCPЁЭANЃЌKЪЧAPЕФжаЕуЃЌ
ЁрCK=BK=AK=PKЃЌ
ЁрЕуAЁЂBЁЂPЁЂCдквдKЮЊдВаФЃЌ ![]() APЮЊАыОЖЕФдВЩЯЃЌ
APЮЊАыОЖЕФдВЩЯЃЌ
ЁпЁЯMAN=60ЃЌ
ЁрЁЯBKC=120ЃЌ
ЁрЁЯKBC=30ЁуЃЌ
ЁпBC=2ЃЌ
ЁрBH=CH=![]() ЃЌ
ЃЌ
Ёпcos30Ёу=![]() =
=![]() ЃЌ
ЃЌ
ЁрBK=![]() ЃЌ
ЃЌ
ЁрCK=BK=![]() AP=
AP=![]() ЃЌМДAP=
ЃЌМДAP=![]() .
.
ЫљвддкећИіЛЌЖЏЙ§ГЬжаЃЌPЁЂAСНЕуМфЕФОрРыБЃГжВЛБфЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ