题目内容
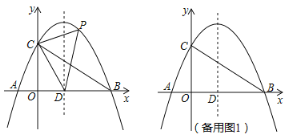
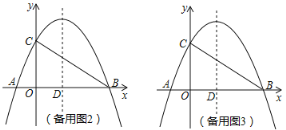
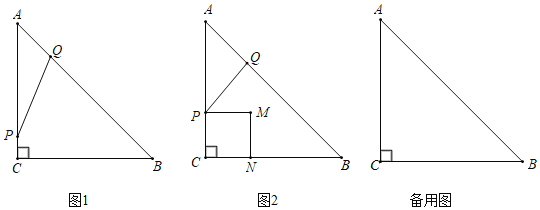
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=6cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以![]() cm/s的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为t(s)
cm/s的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为t(s)
(1)当t=3时,线段PQ的长为 cm;
(2)是否存在某一时刻t,使点B在线段PQ的垂直平分线上?若存在,求出t的值;若不存在,请说明理由;
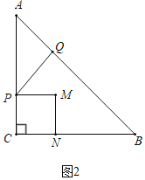
(3)如图2,以PC为边,往CB方向作正方形CPMN,设四边形CPMN与Rt△ABC重叠部分的面积为S,求S关于t的函数关系式.
【答案】(1)3;(2)存在,理由见解析, t=(12﹣6![]() )s;(3)S=t2(0<t≤3)或S=﹣t2+12t﹣18(3<t≤6)
)s;(3)S=t2(0<t≤3)或S=﹣t2+12t﹣18(3<t≤6)
【解析】
(1)由题意得:当t=3时,PC=3=![]() AC,AQ=3
AC,AQ=3![]() =
=![]() AB,即P、Q分别为AC、AB的中点,得出PQ为△ABC的中位线,得出PQ=
AB,即P、Q分别为AC、AB的中点,得出PQ为△ABC的中位线,得出PQ=![]() BC=3即可;
BC=3即可;
(2)由勾股定理得出方程,解方程即可;
(3)分两种情况,由正方形面积公式和三角形面积公式,即可得出答案.
(1)∵∠C=90°,AC=BC=6,
∴AB=![]() =6
=6![]() ,
,
当t=3时,PC=3=![]() AC,AQ=3
AC,AQ=3![]() =
=![]() AB,
AB,
即P、Q分别为AC、AB的中点,
∴PQ为△ABC的中位线,
∴PQ=![]() BC=3(cm);
BC=3(cm);
故答案为:3;
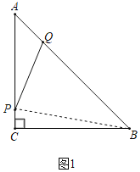
(2)存在.理由如下:
连接BP.如图1,
在Rt△ACB中,∵AC=BC=6,∠C=90°,
∴AB=6![]() ,
,
若点B在线段PQ的垂直平分线上,
则BP=BQ,
∵AQ=![]() t,CP=t,
t,CP=t,
∴BQ=6![]() ﹣
﹣![]() t,
t,
∵PB2=62+t2,
∴(6![]() ﹣
﹣![]() t)2=62+t2,
t)2=62+t2,
整理得:t2﹣24t+36=0,
解得:t=12﹣6![]() 或t=12+6
或t=12+6![]() (舍去),
(舍去),
∴t=(12﹣6![]() )s时,点B在线段PQ的垂直平分线上.
)s时,点B在线段PQ的垂直平分线上.
(3)分两种情况:
①当0<t≤3时,如图2:
S=正方形CPMN的面积=t2;
②当3<t≤6时,如图3:
∵PC=t,AC=6,
∴AP=6﹣t
∵∠C=∠APM=∠M=90°,∠A=∠EFM=45°,
∴△APE∽△FME∽△ACB,并且都是等腰直角三角形
∴PE=AP=6﹣t,
∴EM=FM=t﹣(6﹣t)=2t﹣6,
∴S=S正方形CPMN﹣SRt△EFM =t2﹣![]() (2t﹣6)2=﹣t2+12t﹣18;
(2t﹣6)2=﹣t2+12t﹣18;
综上所述,S关于t的函数关系式为:S=t2(0<t≤3)或S=﹣t2+12t﹣18(3<t≤6).


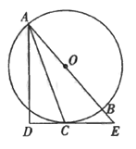
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?