题目内容
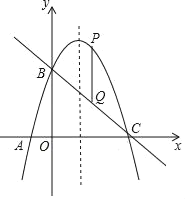
【题目】已知二次函数y=ax2+bx+3的图象经过A(﹣1,0)、C(3,0)、并且与y轴相交于点B,点P是直线BC上方的抛物线上的一动点,PQ∥y轴交直线BC于点Q.
(1)求此二次函数的表达式;
(2)求线段PQ的最大值;
(3)在抛物线的对称轴上,是否存在点M,使△MAB为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)![]() ;(3)M1(1,1),M2(1,
;(3)M1(1,1),M2(1,![]() ),M3(1,﹣
),M3(1,﹣![]() ),M4(1,0).
),M4(1,0).
【解析】
(1)利用待定系数法确定函数关系式即可;(2)设P(﹣m,﹣m2+2m+3),Q(m,﹣m+3).利用两点间的距离公式得到PQ=﹣m2+3m,再利用配方法求得最值即可;(3)分①MA=MB, ②MA=AB,③AB=MB三种情况求点M的坐标即可.
解:(1)∵二次函数y=ax2+bx+3的图象经过A(﹣1,0),C(3,0).
∴![]()
解得![]() .
.
∴此二次函数表达式为y=﹣x2+2x+3.
(2)∵设直线BC为y=kx+b,因其经过B(0,3),C(3,0),
∴![]() .
.
解得k=﹣1,b=3
∴直线BC的表达式为y=﹣x+3.
设P(﹣m,﹣m2+2m+3),Q(m,﹣m+3)
PQ=﹣m2+2m+3﹣(﹣m+3)
=﹣m2+3m
=﹣(m﹣![]() )2+
)2+![]() .
.
PQ的最大值为![]() .
.
(3)存在,理由如下:
∵二次函数y=﹣x2+2x+3的对称轴为x=﹣![]() =1,OA=1,OB=3,
=1,OA=1,OB=3,
在Rt△ABO中由勾股定理可得AB=![]() ,AB2=10.
,AB2=10.
设M(1,a),则MA2=22+a2,MB2=12+(a﹣3)2.
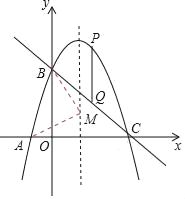
分三种情况讨论:
①MA=MB,22+a2=12+(a﹣3)2,得a=1,
∴M1(1,1);
②MA=AB,22+a2=10,得a=±![]() ,
,
∴M2(1,![]() ),M3(1,﹣
),M3(1,﹣![]() );
);
③AB=MB,12+(a﹣3)2=10,得a=0或a=6,
∴M4(1,0),M5(1,6).
∵M5、A、B三点共线,
∴M5(1,6)舍去.
∴M的坐标为:M1(1,1),M2(1,![]() ),M3(1,﹣
),M3(1,﹣![]() ),M4(1,0).
),M4(1,0).

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案