题目内容
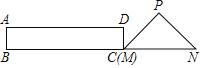
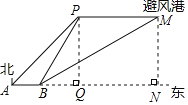
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以80海里/小时的速度继续航行多少小时即可到达?(结果保留根号)

【答案】![]() 小时.
小时.
【解析】
如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,通过解直角△AQP、直角△BPQ求得PQ的长度,即MN的长度,然后通过解直角△BMN求得BM的长度,则易得所需时间.
解:如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,
在直角△AQP中,∠PAQ=45°,则AQ=PQ=60×1+BQ=60+BQ(海里),
所以BQ =PQ-60.
在直角△BPQ中,∠BPQ=30°,则BQ=PQtan30°=PQ(海里),
所以PQ-60=![]() PQ,
PQ,
所以PQ=30(3+![]() )(海里)
)(海里)
所以MN=PQ=30(3+![]() )(海里)
)(海里)
在直角△BMN中,∠MBN=30°,
所以BM=2MN=60(3+![]() )(海里)
)(海里)
所以t=![]() =
=![]() (小时)
(小时)
故答案是:![]() .
.

练习册系列答案
相关题目