题目内容
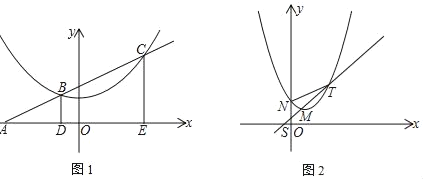
【题目】如图,已知直线:y=kx+3k与x轴交于A点,与抛物线y=![]() +1交于点B、C两点
+1交于点B、C两点
(1)若k=1,求点B、C(点B在点C的左边)的坐标;
(2)过B、C分别作x轴的垂线,垂足分别为点D、E,求ADAE的值;
(3)将抛物线y=![]() +1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
+1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
【答案】(1)点B、C的坐标分别为![]() ;(2)13;(3)t=4m
;(2)13;(3)t=4m
【解析】
(1)联立直线和抛物线表达式即可求解;
(2)设点BC的横坐标分别为x1,x2,将直线表达式与抛物线表达式联立用韦达定理求出:x1+x2=4k,x1x2=4﹣12k,ADAE=(x1+3)(x2+3)即可求解;
(3)求出N(0,![]() +mt+1);再用韦达定理,求出点T的坐标(t+4m,mt+4m2+1),NT∥x轴,则yT=yN,即可求解.
+mt+1);再用韦达定理,求出点T的坐标(t+4m,mt+4m2+1),NT∥x轴,则yT=yN,即可求解.
(1)k=1时,联立直线和抛物线表达式得: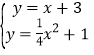 ,解得:x=2±2
,解得:x=2±2![]() ,
,
故:点B、C的坐标分别为(2﹣2![]() ,5﹣2
,5﹣2![]() )、(2+2
)、(2+2![]() ,5+2
,5+2![]() );
);
(2)设点BC的横坐标分别为x1,x2,
y=kx+3k,令y=0,则x=﹣3,即点A(﹣3,0),
将直线表达式:y=kx+3k与抛物线表达式y=![]() +1联立并整理得:
+1联立并整理得:
x2﹣4kx+(4﹣12k)=0,
则:x1+x2=4k,x1x2=4﹣12k,
ADAE=(x1+3)(x2+3)=x1x2+3(x1+x2)+9=4﹣12k+12k+9=13;
(3)设抛物线沿直线向右平移t个单位,相当于同时向上移动了mt个单位,则点M坐标为(t,1+mt),
平移后的抛物线为:y=![]() (x﹣t)2+(1+mt)…①,则点N(0,
(x﹣t)2+(1+mt)…①,则点N(0,![]() +mt+1),
+mt+1),
直线y=mx+1(m>1)…②,
将①②联立并整理得:x2﹣2xt﹣4mx+t2+4mt=0,
x1+x2=2t+4m,
由题意得:x1=xM=t,
∴x2=t+4m=xT,
则点T的坐标为(t+4m,mt+4m2+1),
NT∥x轴,则yT=yN,
即:![]() +mt+1=mt+4m2+1,
+mt+1=mt+4m2+1,
解得:t=4m.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案