题目内容
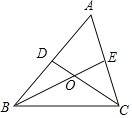
【题目】如图,在△ABC中,BE,CD分别是边AC、AB上的中线,BE与CD相交于点O,BE=6,则OE=_____.
【答案】2
【解析】
如图,过E作EF∥AB,交CD于F点,得到F点为CD的中点,根据三角形中位线定理得出BD:EF=2:1,再证明△EOF∽△BOD得BO:OE=2:1,由相似三角形的性质可得到答案.
如图,过E作EF∥AB,交CD于H点,
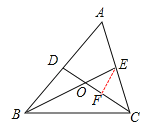
∵BE、CD分别是AC、AB边上的中线,BE与CD相交于点O,
∴AD=BD,F为CD的中点,
∴EF=![]() AD,
AD,
∴EF=![]() BD,即BD:EF=2:1,
BD,即BD:EF=2:1,
∵EF∥AB,
∴∠FEO=∠DBO,
又∠EOF=∠BOD,
∴△EOF∽△BOD,
∴BD:EF=BO:OE=2:1,
∴OE=![]() BO=
BO=![]() BE=
BE=![]() ×6=2,
×6=2,
故答案为:2.

练习册系列答案
相关题目