题目内容
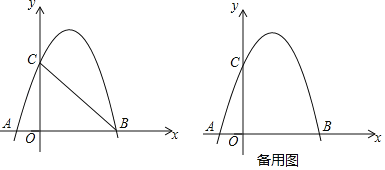
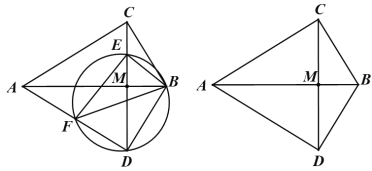
【题目】如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF,
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM正存在点E,使得EF和AB互相平分,求m的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)想办法证明∠BEF=90°即可解决问题(也可以利用圆内接四边形的性质直接证明).
(2)根据两角对应相等两三角形相似证明.
(3)证明四边形AFBE是平行四边形,推出FJ=![]() BD=
BD=![]() m,EF=m,由△ABC∽△CBM,可得BM=
m,EF=m,由△ABC∽△CBM,可得BM=![]() ,由△BEF∽△BCA,推出
,由△BEF∽△BCA,推出![]() ,由此构建方程求解即可.
,由此构建方程求解即可.
(1)证明:由折叠可知,∠ADB=∠ACB=90°
∵∠EFB=∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2) 证明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
(3) 设EF交AB于J.连接AE,如下图所示:

∵EF与AB互相平分,
∴四边形AFBE是平行四边形,
∴∠EFA=∠FEB=90°,即EF⊥AD,
∵BD⊥AD,
∴EF∥BD,
∵AJ=JB,
∴AF=DF,
∴ FJ=![]()
∴ EF=![]()
∵ △ABC∽△CBM
∴ BC:MB=AB:BC
∴ BM=![]() ,
,
∵ △BEJ∽△BME,
∴ BE:BM=BJ:BE
∴ BE=![]() ,
,
∵ △BEF∽△BCA,
∴![]()
即
解得![]() (负根舍去).
(负根舍去).
故答案为:![]()

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案