题目内容
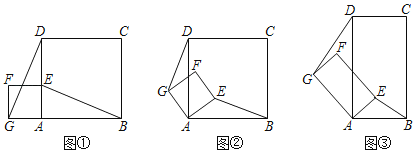
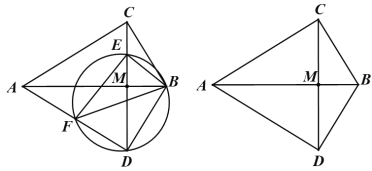
【题目】用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为____________(用含a,b的代数式表示).
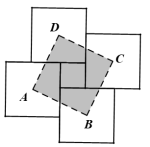
【答案】![]()
【解析】
如图,连接AE、AF,先证明△GAE≌△HAF,由此可证得![]() ,进而同理可得,根据正方形ABCD的面积等于四个相同四边形的面积之和及小正方形的面积即可求得答案.
,进而同理可得,根据正方形ABCD的面积等于四个相同四边形的面积之和及小正方形的面积即可求得答案.
解:如图,连接AE、AF,
∵点A为大正方形的中心,
∴AE=AF,∠EAF=90°,
∴∠AEF=∠AFE=45°,
∵∠GEF=90°,
∴∠AEG=∠GEF-∠AEF=45°,
∴∠AEG=∠AFE,
∵四边形ABCD为正方形,
∴∠DAB=∠EAF=90°,
∴∠GAE=∠HAF,
在△GAE与△HAF中,
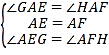
∴△GAE≌△HAF(ASA),
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴同理可得:![]() ,
,
即![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
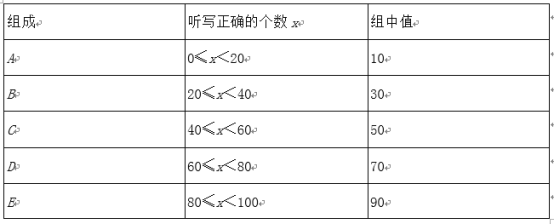
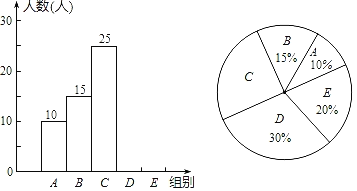
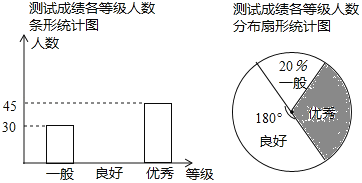
【题目】疫情期间,“线上教学”为我们提供了复习的渠道.学校随机抽取部分学生就“你是否喜欢线上教学”进行了问卷调查,并将调查结果统计后绘制成如下统计表和统计图.
调查结果统计表
类别 | 非常喜欢 | 喜欢 | 一般 | 不喜欢 |
频数 | a | 70 | 20 | 10 |
频率 | 0.5 | b | 0.15 | |
调查结果扇形统计图

(1)在统计表中,a= ;b= ;
(2)在扇形统计图中,对线上教学感觉“一般”所对应的圆心角度数为 ;
(3)已知全校共有3000名学生,试估计“喜欢”线上教学的学生人数.