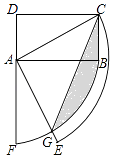题目内容
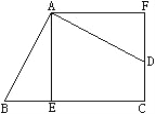
【题目】如图,四边形ABCD的∠BAD=∠C=90,AB=AD,AE⊥BC于E,![]() 旋转后能与
旋转后能与![]() 重合.
重合.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5㎝,求四边形AECF的面积.
【答案】
【1】 点A;
【2】 90度
【3】 25cm2
【解析】
试题(1)旋转中心到对应点的距离相等,因为AB=AD,AE=AF,所以点O是对称中心.而对应线段AB,AD和夹角∠BAD=90°,对应线段AE,AF的夹角∠EAF=90°,所以旋转的角度是90°;
(2)当把△ABE旋转到△ADF的位置后,四边形ABCD就变化为四边形AECF,由题意可得到四边形AECF是正方形,从而由四边形AECF的面积得到四边形ABCD的面积.
试题解析:(1)旋转中心是点A,因为∠BAD=90°,所以旋转了90°.
答:旋转中心是点A,旋转了90°.
(2)因为△BEA≌△DFA,所以AE=AF,∠EAB=∠FAD,而∠BAD=90°,
所以∠EAF=90°,又∠AEC=90°,∠C=90°,
所以四边形AECF是正方形,
因为AE=5,所以正方形AECF的面积为:5×5=25 cm2.
又因为△BEA≌△DFA,所以四边形ABCD的面积是25 cm2.
答:四边形ABCD的面积是25 cm2.

【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数 | 频率 |
篮球 | 30 | 0.25 |
羽毛球 | m | 0.20 |
乒乓球 | 36 | n |
跳绳 | 18 | 0.15 |
其他 | 12 | 0.10 |
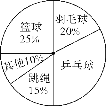
请根据以上图表信息,解答下列问题:
(1)频数分布表中的m=_________,n=_________;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为_________.