题目内容
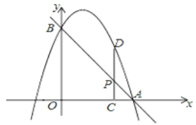
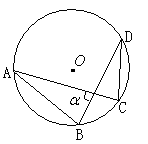
【题目】如图⊙O的半径为1cm,弦AB、CD的长度分别为![]() ,则弦AC、BD所夹的锐角
,则弦AC、BD所夹的锐角![]() = .
= .
【答案】75°
【解析】根据勾股定理的逆定理可证△AOB是等腰直角三角形,故可求∠OAB=∠OBA=45°,又由已知可证△COD是等边三角形,所以∠ODC=∠OCD=60°,根据圆周角的性质可证∠CDB=∠CAB,而∠ODB=∠OBD,所以∠CAB+∠OBD=∠CDB+∠ODB=∠ODC=60°,再根据三角形的内角和定理可求α.
解:连接OA、OB、OC、OD,
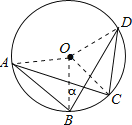
∵OA=OB=OC=OD=1,AB=![]() ,CD=1,
,CD=1,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,
△COD是等边三角形,
∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,
∵∠CDB=∠CAB,∠ODB=∠OBD,
∴α=180°-∠CAB-∠OBA-∠OBD=180°-∠OBA-(∠CDB+∠ODB)=180°-45°-60°=75°.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
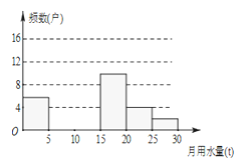
【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | m | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | n |
60≤x<70 | 2 | 0.04 |
请解答以下问题:
(1)求出吗、M,n的值,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?