题目内容
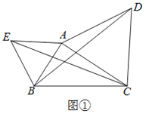
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)

【答案】路灯高AB约为5.8米.
【解析】试题分析:根据EF⊥BC,CD⊥BC,AB⊥BC,得到AB∥CD∥EF,从而得到△ABN∽△ACD,利用相似三角形对应边的比相等列出比例式求解即可.
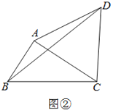
解:如图,设AB= x,
由题意知AB⊥BG,CD⊥BG,FE⊥BG,CD=CE,
∴AB∥CD∥EF,∴BE=AB=x,
∴△ABG∽△FEC
∴![]() ,即
,即![]() ,
,
∴![]() m
m
答:路灯高AB约为5.8米.

练习册系列答案
相关题目
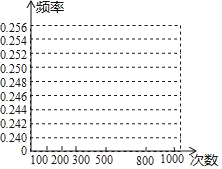
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)