Question

【题目】在直角坐标系xOy中，已知点P是反比例函数y＝(x＞0)图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．

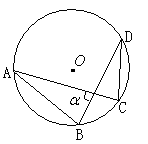
(1)如图1，当⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由；

(2)如图2，当⊙P运动到与x轴相交，设交点为点B、C．当四边形ABCP是菱形时，求出点A、B、C的坐标；

(3)在(2)的条件下，求出经过A、B、C三点的抛物线的解析式．

Answer 1

【答案】(1)四边形OKPA是正方形，理由见解析；(2)A(0，)，B(1，0)，C(3，0)；(3)y＝x2﹣x+．

【解析】

（1）先证明四边形OKPA是矩形，又PA＝PK，故可得四边形OKPA是正方形；

（2）证明△PBC为等边三角形；在Rt△PBG中，∠PBG＝60°，设PB＝PA＝a，BG＝，由勾股定理得：PG＝，所以P（a，），将P点坐标代入y＝，求出PG＝，PA＝BC＝2，又四边形OGPA是矩形，PA＝OG＝2，BG＝CG＝1，故OB＝OG﹣BG＝1，OC＝OG+GC＝3，即可求解；

（3）设二次函数的解析式为：y＝ax2+bx+c，将（2）中三点坐标分别代入，利用待定系数法进行求解即可.

(1)四边形OKPA是正方形，

理由：∵⊙P分别与两坐标轴相切，

∴PA⊥OA，PK⊥OK，

∴∠PAO＝∠OKP＝90°，

又∵∠AOK＝90°，

∴∠PAO＝∠OKP＝∠AOK＝90°，

∴四边形OKPA是矩形，

又∵PA＝PK，

∴四边形OKPA是正方形；

(2)连接PB，过点P作PG⊥BC于G，

∵四边形ABCP为菱形，∴BC＝PA＝PB＝PC，

∴△PBC为等边三角形，

在Rt△PBG中，∠PBG＝60°，

设PB＝PA＝a，BG＝，

由勾股定理得：PG＝，

所以P(a，)，将P点坐标代入y＝，

解得：a＝2或﹣2(舍去负值)，

∴PG＝，PA＝BC＝2，

又四边形OGPA是矩形，PA＝OG＝2，BG＝CG＝1，

∴OB＝OG﹣BG＝1，OC＝OG+GC＝3．

∴A(0，)，B(1，0)，C(3，0)；

(3)二次函数的解析式为：y＝ax2+bx+c，

根据题意得：，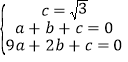

解得：，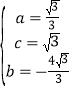

∴二次函数的解析式为：y＝x2﹣x+．