Question

【题目】请认真阅读下面的数学小探究系列，完成所提出的问题：

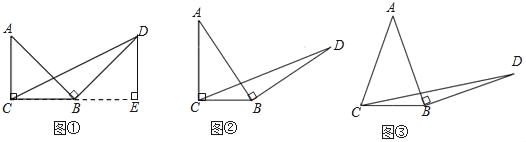
（1）探究1，如图①，在等腰直角三角形ABC中，∠ACB＝90°，BC＝3，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D做BC边上的高DE，则DE与BC的数量关系是　 　，△BCD的面积为　 　；

（2）探究2，如图②，在一般的Rt△ABC中，∠ACB＝90°，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，请用含a的式子表示△BCD的面积，并说明理由；

（3）探究3：如图③，在等腰三角形ABC中，AB＝AC，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，试探究用含a的式子表示△BCD的面积，要有探究过程．

Answer 1

【答案】（1）DE=BC，△BCD的面积为；（2）△BCD的面积为，理由详见解析；（3）△BCD的面积为，理由详见解析.

【解析】

（1）如图1，过点D作BC的垂线，与BC的延长线交于点E，由垂直的性质就可以得出△ABC≌△BDE，就有DE＝BC＝3．进而由三角形的面积公式得出结论；

（2）如图2，过点D作BC的垂线，与BC的延长线交于点E，由垂直的性质就可以得出△ABC≌△BDE，就有DE＝BC＝a．进而由三角形的面积公式得出结论；

（3）如图3，过点A作AF⊥BC与F，过点D作DE⊥BC的延长线于点E，由等腰三角形的性质可以得出BFBC，由条件可以得出△AFB≌△BED就可以得出BF＝DE，由三角形的面积公式就可以得出结论．

（1）如图1，过点D作DE⊥CB交CB的延长线于E，∴∠BED＝∠ACB＝90°，由旋转知：AB＝BD，∠ABD＝90°，∴∠ABC+∠DBE＝90°．

∵∠A+∠ABC＝90°，∴∠A＝∠DBE．

在△ABC和△BDE中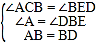，∵，∴△ABC≌△BDE（AAS），∴BC＝DE＝3．

∵S△BCDBCDE，∴S△BCD×32=；

（2）△BCD的面积为．理由如下：

如图2，过点D作BC的垂线，与BC的延长线交于点E，∴∠BED＝∠ACB＝90°．

∵线段AB绕点B顺时针旋转90°得到线段BE，∴AB＝BD，∠ABD＝90°，∴∠ABC+∠DBE＝90°．

∵∠A+∠ABC＝90°，∴∠A＝∠DBE．

在△ABC和△BDE中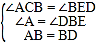，∵，∴△ABC≌△BDE（AAS），∴BC＝DE＝a．

∵S△BCDBCDE，∴S△BCD；

（3）如图3，过点A作AF⊥BC与F，过点D作DE⊥BC的延长线于点E，∴∠AFB＝∠E＝90°，BFBCa，∴∠FAB+∠ABF＝90°．/p>

∵∠ABD＝90°，∴∠ABF+∠DBE＝90°，∴∠FAB＝∠EBD．

∵线段BD是由线段AB旋转得到的，∴AB＝BD．

在△AFB和△BED中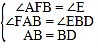，∵，∴△AFB≌△BED（AAS），∴BF＝DEa．

∵S△BCDBCDEaaa2，∴△BCD的面积为．