题目内容
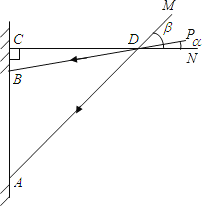
【题目】在一次综合实践课上,同学们为教室窗户设计一个遮阳篷,小明同学绘制的设计图如图所示,其中AB表示窗户,且AB=2米,BCD表示直角遮阳蓬,已知当地一年中正午时刻太阳光与水平线CD的最小夹角∠PDN=18.6°,最大夹角∠MDN=64.5°.请你根据以上数据,帮助小明同学计算出遮阳篷中CD的长是多少米?(结果精确到0.1)(参考数据:sin18.6°≈0.32,tan18.6°≈0.34,sin64.5°≈0.90,tan64.5°≈2.1)

【答案】CD的长约为1.1米.
【解析】
解直角三角求出BC=0.34x米,AC=2.1x米,得出方程,求出方程的解即可.
设CD=x米,
在Rt△BCD中,∠BCD=90°,∠CDB=∠PDN=18.6°,CB=CD×tan18.6°≈0.34x米,
在Rt△ACD中,∠ACD=90°,∠CDA=∠MDN=64.5°,AC=CD×tan64.5°≈2.1x米,
∵AB=2米,AB=AC﹣BC,
∴2.1x﹣0.34x=2,
解得:x≈1.1,
即遮阳篷中CD的长约为1.1米.

练习册系列答案
相关题目