��Ŀ����
����Ŀ����ͼ���ı���ABCDΪ���Σ�AB��4cm��AD��3cm������M��N�ֱ��D��Bͬʱ����������1cm/����ٶ��˶�����M��DA����յ�A�˶�����N��BC���յ�C�˶�������N��NP��BC����AC�ڵ�P������MP����֪�˶���ʱ��Ϊt�루0��t��3����
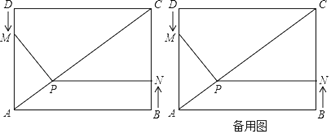
��1����t��1��ʱ�����PN�ij���
��2�����ı���CDMP�����Ϊs������s��t�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��tʹ�ı���CDMP��������ı���ABCD�������Ϊ3��8�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��4���ڵ�M��N�˶������У���MPA�ܷ��Ϊһ�����������Σ����ܣ����������t�Ŀ���ֵ�������ܣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3�����ڣ�
����3�����ڣ�![]() ����4���ܣ���t��1��t��
����4���ܣ���t��1��t��![]() ��t��
��t��![]() ʱ����MPA�ǵ���������.
ʱ����MPA�ǵ���������.
��������
(1)��t��1֪BN��1��CN��BC��BN��2��֤��PNC�ס�ABC��![]() ���ݴ˿ɵô𰸣�
���ݴ˿ɵô𰸣�
(2)�ӳ�NP��AD�ڵ�Q����PQ��AD������PNC�ס�ABC��![]() ���ݴ˵ó�PN��4��
���ݴ˵ó�PN��4��![]() t��PQ��
t��PQ��![]() t������S�ı���CDMP��S��ACD��S��AMP�ɵã�
t������S�ı���CDMP��S��ACD��S��AMP�ɵã�
(3)�������ABCD�������Ȼ��������ɵù���t�ķ��̣��ⷽ�̼�����ô𰸣�
(4)����Ҫ�������������MP��PA����ôAQ��BN��![]() AM������x�ֱ��ʾ��BN��AM�ij���Ȼ���������������ϵ�����x��ֵ����MA��MP����ֱ��������MQP�У�MQ��MA��BN��PQ��AB��PN���ݹ��ɶ����������x��ֵ����MA��PA�����ѵó�AP��
AM������x�ֱ��ʾ��BN��AM�ij���Ȼ���������������ϵ�����x��ֵ����MA��MP����ֱ��������MQP�У�MQ��MA��BN��PQ��AB��PN���ݹ��ɶ����������x��ֵ����MA��PA�����ѵó�AP��![]() BN��Ȼ����x��ʾ��AM�ij����������x��ֵ��
BN��Ȼ����x��ʾ��AM�ij����������x��ֵ��
(1)��t��1ʱ��BN��1��CN��BC��BN��2��
��PN��BC��
���PNC����B��90����
��PN��AB��
���PNC�ס�ABC��
��![]() ����
����![]() ��
��
��PN��![]() ��
��
(2)��ͼ���ӳ�NP��AD�ڵ�Q����PQ��AD��

������֪��DM��BN��t��AM��CN��3��t��
��PN��AB��
���PNC�ס�ABC��
��![]() ����
����![]() ��
��
��ã�PN��![]() (3��t)��4��
(3��t)��4��![]() t��
t��
��PQ��AD��
���QAB����B����NQA��90����
���ı���ABNQ�Ǿ��Σ�
��AB��QN��4��
��PQ��QN��PN��4��(4��![]() t)��
t)��![]() t��
t��
���ı���CDMP�����s��![]() ��3��4��
��3��4��![]() ��(3��t)��
��(3��t)��![]() t��
t��![]() t2��2t+6��
t2��2t+6��
(3)��S����ABCD��3��4��12��
�� ��
��
��ã�t��![]() ��
��
����t��![]() ʱ�ı���CDMP��������ı���ABCD�������Ϊ3��8��
ʱ�ı���CDMP��������ı���ABCD�������Ϊ3��8��
(4)��MPA�ܳ�Ϊ���������Σ�����������������·���˵����
����PM��PA��
��PQ��MA��
���ı���ABNQ�Ǿ��Σ�
��QA��NB��t��
��MQ��QA��t��
����DM+MQ+QA��AD
��3t��3����t��1
����MP��MA����MQ��3��2t��PQ��![]() t��MP��MA��3��t��
t��MP��MA��3��t��
��Rt��PMQ�У��ɹ��ɶ����ã�MP2��MQ2+PQ2
��(3��t)2��(3��2t)2+(![]() t)2��
t)2��
��ã�t��![]() (t��0�������⣬��ȥ)��
(t��0�������⣬��ȥ)��
����AP��AM��
������ɵã�AP��![]() t��AM��3��t
t��AM��3��t
��![]() t��3��t��
t��3��t��
��ã�t��![]() ��
��
������������t��1��t��![]() ��t��
��t��![]() ʱ����MPA�ǵ��������Σ�
ʱ����MPA�ǵ��������Σ�

 ͬ������ϵ�д�
ͬ������ϵ�д�