题目内容
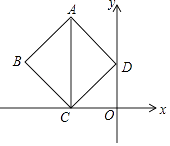
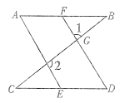
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.
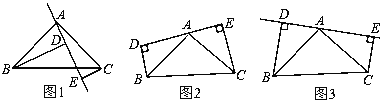
(1)求证:BD=DE+CE;
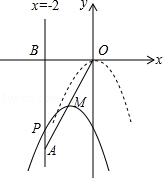
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
【答案】(1)证明见解析;(2)BD=DE+CE;(3)BD=DE+CE.
【解析】
试题分析:本题考查了全等三角形的判定和性质,涉及到直角三角形的性质、余角和补角的性质等知识点,熟练掌握全等三角形的判定方法是解题的关键.
(1)根据已知条件易证得∠BAD=∠ACE,且根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(2)BD=DE+CE.根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(3)同上理,BD=DE+CE仍成立.
试题解析:(1)在△ABD和△CAE中,
∵∠CAD+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAD=∠ABD.
又∠ADB=∠AEC=90°,AB=AC,∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.又AE=AD+DE,∴AE=DE+CE,即BD=DE+CE.
(2)BD=DE﹣CE.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.又AB=AC,∠ADB=∠CEA=90°,∴△ADB≌△CEA.∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,即 BD=DE﹣CE
(3)同理:BD=DE﹣CE.

【题目】某校需要招聘一名教师,对三名应聘者进行了三项素质测试![]() 下面是三名应聘者的综合测试成绩:
下面是三名应聘者的综合测试成绩:
应聘者 成绩 项目 | A | B | C |
基本素质 | 70 | 65 | 75 |
专业知识 | 65 | 55 | 50 |
教学能力 | 80 | 85 | 85 |
(1)如果根据三项测试的平均成绩确定录用教师,那么谁将被录用?
(2)学校根据需要,对基本素质、专业知识、教学能力的要求不同,决定按2:1:3的比例确定其重要性,那么哪一位会被录用?