题目内容
【题目】一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形.在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个在大矩形的面积,则n的最小值是 ( )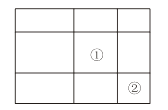
A.3
B.4
C.5
D.6
【答案】A
【解析】解:要算出这个在大矩形的面积,就需要知道大矩形的长和宽.
如图: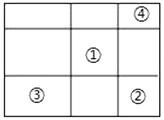
假设已知小矩形①的周长为4x,小矩形③周长为2y,小矩形④周长为2z;
则可得出①的边长以及③和④的邻边和,分别为x、y、z;
设小矩形②的周长为4a,则②的边长为a,可得③、④都有一边长为a
则③和④的另一条边长分别为:y﹣a,z﹣a,
故大矩形的边长分别为:y﹣a+x+a=y+x,z﹣a+x+a=z+x,
故大矩形的面积为:(y+x)(z+x),当x,y,z都为已知数时,即可算出大正方形的面积,
故n的最小值是3.
故选:A.
【考点精析】通过灵活运用推理与论证,掌握一个正确的论证必须满足两个条件:1、论据(前提)是真实的;2、论证方式(推理形式)是正确的(有效的)即可以解答此题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
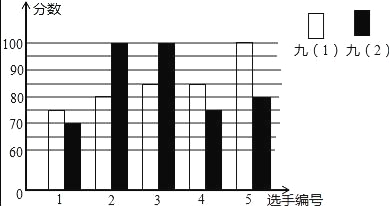
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
九(1) | 85 | |
九(2) | 100 |
(2)通过计算得知九(2)班的平均成绩为85分,请计算九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?