题目内容
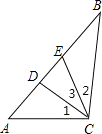
如图，已知△ABC的角平分线BD与∠ACB的外角平分线交于D点，DE∥BC交于E，交AC于F，求证：EF=BE-CF．
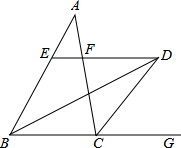
证明：∵BD平分∠ABC，
∴∠ABD=∠CBD，
∵DE∥BC，
∴∠EDB=∠CBD，
∴∠ABD=∠EDB，
∴DE=BE，
同理DF=CF，
∵EF=DE-DF，
∴EF=BE-CF．
∴∠ABD=∠CBD，
∵DE∥BC，
∴∠EDB=∠CBD，
∴∠ABD=∠EDB，
∴DE=BE，
同理DF=CF，
∵EF=DE-DF，
∴EF=BE-CF．
练习册系列答案
全程金卷系列答案
相关题目
