题目内容
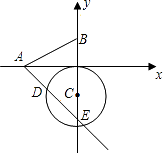
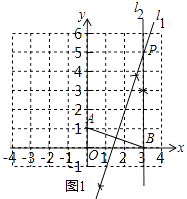
【题目】如图1，在平面直角坐标系xOy中，点A的坐标为（0，1），取一点B（b，0），连接AB，做线段AB的垂直平分线l1 ， 过点B作x轴的垂线l2 ， 记l1 ， l2的交点为P．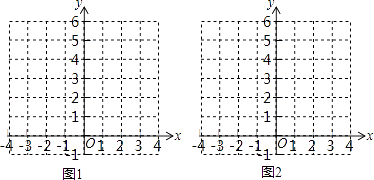
（1）当b=3时，在图1中补全图形（尺规作图，不写作法，保留作图痕迹）；
（2）小慧多次取不同数值b，得出相应的点P，并把这些点用平滑的曲线连接起来发现：这些点P竟然在一条曲线L上！
①设点P的坐标为（x，y），试求y与x之间的关系式，并指出曲线L是哪种曲线；
②设点P到x轴，y轴的距离分别是d1 ， d2 ， 求d1+d2的范围，当d1+d2=8时，求点P的坐标；
③将曲线L在直线y=2下方的部分沿直线y=2向上翻折，得到一条“W”形状的新曲线，若直线y=kx+3与这条“W”形状的新曲线有4个交点，直接写出k的取值范围．
【答案】
（1）解：线段AB的垂直平分线l1，过点B作x轴的垂线l2，直线l1与l2的交点为P，如图所示，
（2）解：①当x＞0时，如图2中，连接AP，作PE⊥y轴于E，
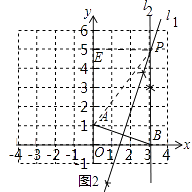
∵l1垂直平分AB，
∴PA=PB=y，
在RT△APE中，∵EP=BO=x，AE=OE﹣OA=y﹣1，PA=y，
∴y2=x2+（y﹣1）2，
∴y= 
x2+ ，
当x＜0时，点P（x，y）同样满足y= x2+ ，
∴曲线l就是二次函数y= x2+ 即曲线l是抛物线．
②∵d1= x2+ ，d2=|x|，
∴d1+d2= x2+ +|x|，
当x=0时，d1+d2有最小值 ，
∴d1+d2≥ ，
∵d1+d2=8，则 x2+ +|x|=8，
当x≥0时，原方程化为 x2+ +x﹣8=0，解得x=3或（﹣5舍弃），
当x＜0时，原方程化为 x2+ ﹣x﹣8=0，解得x=﹣3或（5舍弃），
∵x=±3时，y=5，
∴点P坐标（3，5）或（﹣3，5）．
③如图3中，
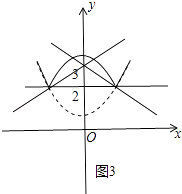
把y=2代入y= x2+ ，解得x= 
，
∴直线y=2与抛物线y= x2+ 的两个交点为（﹣ 
，2）和（ ，2）．
当直线y=kx+3经过点（﹣ ，2）时，2=﹣ k+3
∴k= 
，
当直线y=kx+3经过点（ ，2）时，2= k+3，
∴k=﹣ ，
∴直线y=kx+3与这条“W”形状的曲线有四个交点时，k的取值范围是：﹣ ＜k＜ ．
【解析】（1）利用尺规作出线段AB的垂直平分线，过点B作出x轴的垂线即可．（2）①分x＞O或x＜0两种情形利用勾股定理求出x与y的关系即可解决问题．②由题意得d1+d2= x2+ +|x|，列出方程即可解决问题．③求出直线y=2与抛物线y= x2+ 的两个交点为（﹣ ，2）和（ ，2），利用这两个特殊点，求出k的值即可解决问题．
