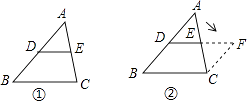题目内容
【题目】在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( ) 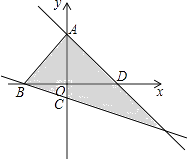
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵AB=5,OA=4,
∴OB= ![]() =3,
=3,
∴点B(﹣3,0).
∵OA=OD=4,
∴点A(0,4),点D(4,0).
设直线AD的解析式为y=kx+b,
将A(0,4)、D(4,0)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线AD的解析式为y=﹣x+4;
设直线BC的解析式为y=mx+n,
将B(﹣3,0)、C(0,﹣1)代入y=mx+n,
![]() ,解得:
,解得: 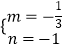 ,
,
∴直线BC的解析式为y=﹣ ![]() x﹣1.
x﹣1.
联立直线AD、BC的解析式成方程组,
 ,解得:
,解得: 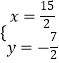 ,
,
∴直线AD、BC的交点坐标为( ![]() ,﹣
,﹣ ![]() ).
).
∵点(a,b)在如图所示的阴影部分内部(不包括边界),
∴﹣3<a< ![]() .
.
故选D.
【考点精析】通过灵活运用不等式的解集在数轴上的表示,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法 |

请你利用小亮的发现解决下列问题:
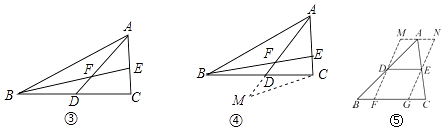
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .