题目内容
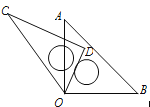
【题目】阅读与理解: 图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
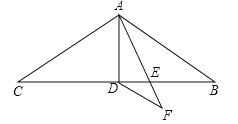
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?
【答案】
(1)解:BE=AD.
∵△C′DE绕点C按顺时针方向旋转30°,
∴∠BCE=∠ACD=30度,
∵△ABC与△C′DE是等边三角形,
∴CA=CB,CE=CD,
∴△BCE≌△ACD,
∴BE=AD
(2)解:BE=AD.
∵△C′DE绕点C按顺时针方向旋转的角度为α,
∴∠BCE=∠ACD=α,
∵△ABC与△C′DE是等边三角形,
∴CA=CB,CE=CD,
∴△BCE≌△ACD,
∴BE=AD.
猜想与发现:
当α为180°时,线段AD的长度最大,等于a+b;当α为0°(或360°)时,线段AD的长度最小,等于a﹣b
【解析】(1)根据旋转的性质及等边三角形的性质,利用SAS判定△BCE≌△ACD,根据全等三角形的对应边相等,可得到BE=AD.(2)围绕证明△BCE≌△ACD,根据SAS寻找全等的条件,方法不变.
【考点精析】关于本题考查的等边三角形的性质和旋转的性质,需要了解等边三角形的三个角都相等并且每个角都是60°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.