题目内容
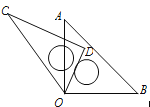
【题目】如图所示,将一副直角三角板的顶点叠合在一起,记为点O(∠C=30°,∠A=45°).
(1)当∠AOC=45°时,求∠DOB的度数;
(2)请探究∠AOC和∠DOB之间满足的数量关系,并说明理由.
【答案】(1)∠DOB=75°(2)∠DOB-∠AOC=30°,理由见解析.
【解析】
(1)根据三角板的各角度数,明确∠COD=60°,∠AOC=45°,表示出∠DOB= ∠AOB-∠AOD即可解题;(2)由∠AOB永远比∠COD大30°可知,当两个角减掉相同角度后,关系仍成立即可解题.
解:(1)解: 因为∠COD=60°,∠AOC=45°
所以∠AOD= ∠COD-∠AOC=15°
因为∠AOB=90°
所以∠DOB= ∠AOB-∠AOD=75°
(2)解:因为∠COD=60°
所以∠AOD= ∠COD-∠AOC=60°-∠AOC
因为∠AOB=90°
所以∠DOB= ∠AOB-∠AOD=90°-(60°- ∠AOC)=30°+∠AOC
即∠DOB-∠AOC=30°

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目