��Ŀ����
����Ŀ�����мס��������������ֱ�װ�н�ˮ�ܺͳ�ˮ�� ���������Ľ���ˮ�ٶȲ��䣬�ȴ��������Ľ�ˮ�ܣ�2����ʱ�ٴ������Ľ�ˮ�ܣ��ֹ�2���ӹرռ������Ľ�ˮ�ܣ��ٹ�4����ͬʱ�������Ľ�����ˮ�ܡ�ֱ��12����ʱ��ͬʱ�ر��������Ľ���ˮ�ܡ��ر�ˮ�ܵ�ʱ����Բ��ơ������е�ˮ��y(��)��������עˮʱ��x(��)֮��Ĺ�ϵ��ͼ��ʾ
��1����������Ľ�����ˮ�ٶȣ�
��2����![]() ʱ������������Ƿ������������ˮ����ȣ������ڣ������ʱx��ֵ��
ʱ������������Ƿ������������ˮ����ȣ������ڣ������ʱx��ֵ��
��3�����������������װһ����ˮ�ܣ����ˮ�ٶ���2�����֣���ʹ��������12����ʱ��ˮ����� ����Ӧ���ڵڼ����Ӵ˽�ˮ�ܣ�
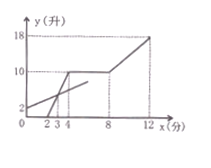
���𰸡���1��5,3����2��8����3��10
��������
��1������ͼʾ֪������������2�����ڽ�ˮ��Ϊ10����
��2����ͼ��֪���������ڵ�3����ʱˮ��Ϊ��5����3-2��=5����������A��3��5������y��=kx+b��k��0�������ô���ϵ������øú�������ʽ����y=10������ֵ����.
��3������t����ʱ�����������������ﵽ18��ʱ�г���ʽ.
(1)�Ľ�ˮ�ٶȣ�![]() =5(��/��)��
=5(��/��)��
�ij�ˮ�ٶȣ�5![]() =3(��/��)��
=3(��/��)��
(2)���ڡ�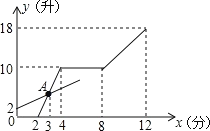
��ͼ��֪,�������ڵ�3����ʱˮ��Ϊ��5��(32)=5(��),��A(3,5).
��y��=kx+b(k��0)��������ã�
3k+b=5��b=2��
��ã�{k=1b=2��
����y��=x+2.
��y��=10ʱ��x=8.
������������ˮ�ܴ�8����ʱ��������ˮ����ȣ�
(3)��x=12ʱ��y��=18.
����t���Ӵ���ˮ��.
����ɵ�,2+12+2(12-t)=18
��t=10.
Ӧ�ڵ�ʮ���Ӵ˽�ˮ��.








