题目内容
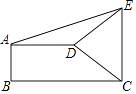
【题目】如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.
求证:(1)BC=AD;
(2)△OAB是等腰三角形.

【答案】证明:(1)∵AC⊥BC,BD⊥AD,∴△ABC与△BAD是直角三角形,
在△ABC和△BAD中,∵ AC=BD ,AB=BA,∠ACB=∠BDA =900,
∴△ABC≌△BAD(HL)。∴BC=AD。
(2)∵△ABC≌△BAD,∴∠CAB=∠DBA,∴OA=OB。
∴△OAB是等腰三角形。
【解析】全等三角形的判定和性质,等腰三角形的判定。
(1)根据AC⊥BC,BD⊥AD,得出△ABC与△BAD是直角三角形,再由AC=BD,AB=BA,根据HL得出△ABC≌△BAD,即可证出BC=AD。
(2)根据△ABC≌△BAD,得出∠CAB=∠DBA,从而证出OA=OB,△OAB是等腰三角形。

练习册系列答案
相关题目
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
【题目】甲、乙、丙三人到文具店购买同一种笔记本和钢笔,甲、乙两人购买的数量及总价分别如表:
甲 | 乙 | |
笔记本(本) | 20 | 15 |
钢笔(支) | 12 | 25 |
总价(元) | 312 | 330 |
(1)求笔记本和钢笔的单价;
(2)丙购买24本笔记本和若干支钢笔共花去526元,甲发现丙的总价算错了,请通过计算加以说明.