题目内容
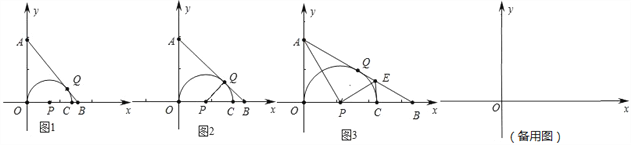
【题目】在一次课题学习活动中,老师提出了如下问题:如图,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() .请你探究
.请你探究![]() 与
与![]() 存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是
存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是![]() ,而要证明结论
,而要证明结论![]() ,就需要证明
,就需要证明![]() 和
和![]() 所在的两个三角形全等,但
所在的两个三角形全等,但![]() 和
和![]() 显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点
显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点![]() 是边
是边![]() 的中点,小明想到的方法是如图2,取
的中点,小明想到的方法是如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() .从而得到
.从而得到![]() .请你参考小明的方法解决下列问题.
.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点![]() 是边
是边![]() 的中点”改为“点
的中点”改为“点![]() 是边
是边![]() 上的任意一点”,其余条件不变,证明结论
上的任意一点”,其余条件不变,证明结论![]() 仍然成立;
仍然成立;
(2)如图4,若把条件“点![]() 是边
是边![]() 的中点”改为:“点
的中点”改为:“点![]() 是边
是边![]() 延长线上的一点”,其余条件仍不变,那么结论
延长线上的一点”,其余条件仍不变,那么结论![]() 是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
是否还成立?若成立,请完成证明过程,若不成立,请说明理由.




【答案】(1)正确,见解析;(2)正确,见解析
【解析】
(1)在AB上取点![]() ,连接
,连接![]() ,证明△PAE≌△CEF即可;
,证明△PAE≌△CEF即可;
(2)延长BA至![]() ,使
,使![]() =CE,连接
=CE,连接![]() ,证明△ANE≌△ECF即可.
,证明△ANE≌△ECF即可.
解:(1)正确.
证明:在AB上取一点M,使AM=EC,连接ME.
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
∴BM=BE,
∴∠BME=45°,
∴∠AME=135°,
∵CF是外角平分线,
∴∠DCF=45°,
∴∠ECF=135°,
∴∠AME=∠ECF,
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∴△AME≌△ECF(ASA),
∴AE=EF.
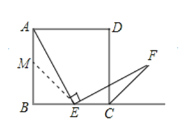
(2)正确.
证明:在BA的延长线上取一点N.
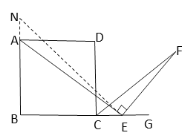
使AN=CE,连接NE.
∴BN=BE,
∴∠N=∠NEC=45°,
∵CF平分∠DCG,
∴∠FCE=45°,
∴∠N=∠ECF,
∵四边形ABCD是正方形,
∴AD∥BE,
∴∠DAE=∠BEA,
即∠DAE+90°=∠BEA+90°,
∴∠NAE=∠CEF,
∴△ANE≌△ECF(ASA)
∴AE=EF.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案