题目内容
【题目】某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:

已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系,并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F.当∠PEQ=70°时,请求出∠PFQ的度数.
【答案】(1)∠PEQ=∠APE+∠CQE,理由见解析;(2)∠PFQ=110°;(3)∠PFQ=145°.
【解析】
(1)
过E点作EH∥AB,再利用平行线性质,两直线平行内错角相等,可得到∠PEQ=∠APE+∠CQE.
(2)过点E作EM∥AB,利用平行线性质,角平分线定义可以得到角的关系,可得到∠PEQ=∠APE+∠CQE=140°,再作NF∥AB,利用平行线性质,角平分线定义可以得到角的关系,得到,∠PFQ=∠BPF+∠DQF的度数.
(3)过点E作EM∥CD,如图,设∠CQM=α,∴∠DQE=180°-α,再利用角平分线性质得到∠DQH=90°-![]() α,∠FQD=90°+
α,∠FQD=90°+![]() α,再利用平行线性质、角平分线定义∠BPF=
α,再利用平行线性质、角平分线定义∠BPF=![]() ∠BPE=55°-
∠BPE=55°-![]() α,作NF∥AB,∠PFQ=∠BPF+∠DQF即可求出答案.
α,作NF∥AB,∠PFQ=∠BPF+∠DQF即可求出答案.
(1)
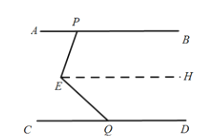
过E点作EH∥AB,
∠PEQ=∠APE+∠CQE,理由如下:
过点E作EH∥AB ∴∠APE=∠PEH ∵EH∥AB,AB∥CD ∴EH∥CD
∴∠CQE=∠QEH,∵∠PEQ=∠PEH+∠QEH ∴∠PEQ=∠APE+∠CQE
(2)
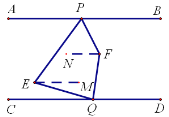
过点E作EM∥AB,如图,同理可得,∠PEQ=∠APE+∠CQE=140°
∵∠BPE=180°-∠APE,∠EQD=180°-∠CQE,∴∠BPE+∠EQD=360°-(∠APE+∠CQE)=220°,∵PF平分∠BPE,QF平分∠EQD ∴∠BPF=![]() ∠BPE,∠DQF=
∠BPE,∠DQF=![]() ∠EQD
∠EQD
∴∠BPF+∠DQF=![]() (∠BPE+∠EQD)=110°,作NF∥AB,同理可得,∠PFQ=∠BPF+∠DQF=110°
(∠BPE+∠EQD)=110°,作NF∥AB,同理可得,∠PFQ=∠BPF+∠DQF=110°
(3)
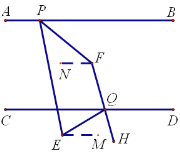
过点E作EM∥CD,如图,设∠CQM=α,∴∠DQE=180°-α,∵QH平分∠DQE,
∴∠DQH=![]() ∠DQE=90°-
∠DQE=90°-![]() α,∴∠FQD=180°-∠DQH=90°+
α,∴∠FQD=180°-∠DQH=90°+![]() α,
α,
∵EM∥CD,AB∥CD ∴AB∥EM,∴∠BPE=180°-∠PEM=180°-(70°+α)=110°-α
∵PF平分∠BPE ∴∠BPF=![]() ∠BPE=55°-
∠BPE=55°-![]() α,
α,
作NF∥AB,同理可得,∠PFQ=∠BPF+∠DQF=145°

 名校课堂系列答案
名校课堂系列答案【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?