题目内容
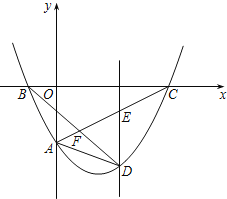
【题目】平面直角坐标系中,A(0,4),点P从原点O开始向x轴正方向运动,设P点横坐标为m,以点P为圆心,PO为半径作⊙P交x 轴另一点为C,过点A作⊙P的切线交 x轴于点B,切点为Q.
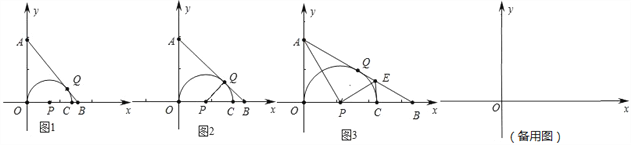
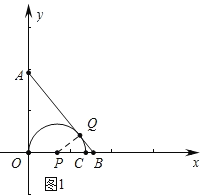
(1)如图1,当B点坐标为(3,0)时,求m;
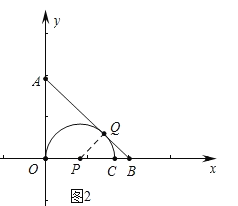
(2)如图2,当△PQB为等腰三角形时,求m;
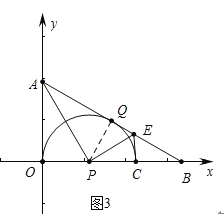
(3)如图3,连接AP,作PE⊥AP交AB于点E,连接CE,求证:CE是⊙P的切线;
(4)若在x轴上存在点M(8,0),在点P整个运动过程中,求MQ的最小值.
【答案】(1)m=![]() (2)m=4
(2)m=4![]() ﹣4(3)证明见解析(4)4
﹣4(3)证明见解析(4)4![]() ﹣4
﹣4
【解析】试题分析: ![]() 如图1中,由
如图1中,由![]()
![]() 由此即可解决问题.
由此即可解决问题.
(2)如图2中,设![]() 则
则![]() 列出方程即可解决问题.
列出方程即可解决问题.
(3)如图3中,连接PQ.只要证明![]() 推出
推出![]() 由此即可证明.
由此即可证明.
(4)以![]() 为圆心
为圆心![]() 为半径画圆交
为半径画圆交![]() 于点
于点![]() ,此时
,此时![]() 最小(两点之间线段最短),设
最小(两点之间线段最短),设![]() 在
在![]() 中,根据
中,根据![]() 列出方程即可解决问题.
列出方程即可解决问题.
试题解析:(1)如图1中,连接PQ.
∵OP⊥OA,
∴AO是P切线,∵AQ是P切线,
∴AO=AQ=4,
∵OA=4,0B=3,
![]()
∴BQ=ABAQ=1,
![]()
![]()
![]()
![]()
![]()
![]()
(2)如图2中,连接PQ.
∵△PQB是等腰直角三角形,
∴OP=PQ=BQ,设OP=PQ=BQ=x,则![]()
则有![]()
![]()
![]()
(3)如图3中,连接PQ.
![]() AQ是切线,
AQ是切线,
![]()
![]()
∴∠EPQ=∠PAQ,
![]()
∴∠EPC=∠PAO,
∵AO、AQ是切线,
∴∠PAO=∠PAQ,
∴∠EPC=∠EPQ,
在△EPC和△EPQ中,
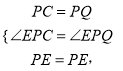
![]()
![]()
∴EC是![]() 的切线.
的切线.
(4)如图4中,
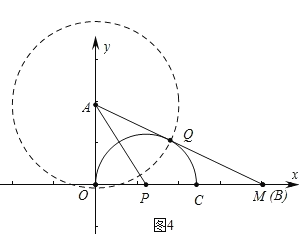
以A为圆心OA为半径画圆交AM于点Q,此时MQ最小(两点之间线段最短),
设QM=x,
在![]() 中,
中, ![]()
![]()
解得![]() 或
或![]() (舍弃),
(舍弃),
∴MQ的最小值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目