Question

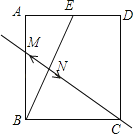
【题目】如图，四边形ABCD内接于⊙O，四边形ABCO是平行四边形，则∠1+∠2= ( )

A.45°B.50°C.60°D.75°

Answer 1

【答案】C

【解析】

根据平行四边形的性质得出∠B=∠AOC，根据圆内接四边形求出∠ADC+∠B=180°，根据圆周角定理得出∠AOC=2∠ADC，求出∠ADC，即可得出答案．

解：连接OD，

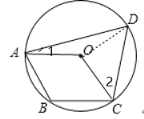
∵AO=OD，OD=OC，
∴∠1=∠ODA，∠2=∠ODC，
∴∠1+2=∠ADC，
∵四边形ABCO是平行四边形，
∴∠B=∠AOC，
∵四边形ABCD是圆内接四边形，
∴∠ADC+∠B=180°，
∵∠ADC=∠AOC，
∴∠ADC=∠B，
即3∠ADC=180°，
∴∠ADC=60°，
即∠1+∠2=60°，
故选：C．