Question

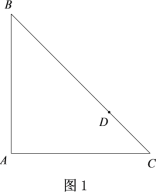
【题目】如图所示，在梯形ABCD中，AD∥BC，AB＝AD，∠BAD的平分线AE交BC于点E，连接DE．

（1）求证：四边形ABED是菱形；

（2）若∠ABC＝60°，CE＝2BE，试判断△CDE的形状，并说明理由．

Answer 1

【答案】见解析

【解析】

试题（1）先证得四边形ABED是平行四边形，又AB=AD， 邻边相等的平行四边形是菱形；

（2）四边形ABED是菱形，∠ABC=60°，所以∠DEC=60°，AB=ED，又EC=2BE，EC=2DE，可得△DEC是直角三角形．

试题解析：梯形ABCD中，AD∥BC，

∴四边形ABED是平行四边形，

又AB=AD，

∴四边形ABED是菱形；

（2）∵四边形ABED是菱形，∠ABC=60°，

∴∠DEC=60°，AB=ED，

又EC=2BE，

∴EC=2DE，

∴△DEC是直角三角形，