题目内容
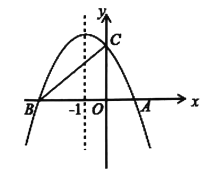
【题目】如图,二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(2,0),点C的坐标为(0,4),它的对称轴是直线x=-1.
的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(2,0),点C的坐标为(0,4),它的对称轴是直线x=-1.
(1)求这个二次函数的解析式;
(2)在第二象限内抛物线上是否存在一点P,使![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 的面积最大值;若没有,请说明理由.
的面积最大值;若没有,请说明理由.
【答案】(1)![]() ;(2)x=-2时,△PBC的面积最大为4.
;(2)x=-2时,△PBC的面积最大为4.
【解析】
(1)利用待定系数法求出即可得出结论;
(2)根据A点坐标及对称轴求出B点坐标,设P点(x,![]() )(-4<x<0),求出S△BPC=-(x+2)2+4,即可求出最大值.
)(-4<x<0),求出S△BPC=-(x+2)2+4,即可求出最大值.
解:(1)根据题意得,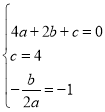 ,
,
解得: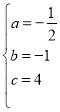 ,
,
∴二次函数的解析式![]() ;
;
(2)如图,存在.

理由如下:
∵A的坐标为(2,0),它的对称轴是直线x=-1.
∴点B的坐标为(-4,0),
设P点(x,![]() )(-4<x<0),
)(-4<x<0),
∵S△BPC=S四边形BPCO-S△BOC
=S△BOP+S△COP-S△BOC
=![]() ×4×(
×4×(![]() )+
)+![]() ×4×(-x)-
×4×(-x)- ![]() ×4×4
×4×4
=-x2-4x
=-(x+2)2+4,
∴x=-2时,△PBC的面积最大为4.

练习册系列答案
相关题目