Question

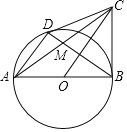
【题目】如图，已知AB是⊙O的直径，CB⊥AB，D为圆上一点，且AD∥OC，连接CD，AC，BD，AC与BD交于点M．

（1）求证：CD为⊙O的切线；

（2）若CD＝AD，求的值．

Answer 1

【答案】（1）见解析；（2）.

【解析】

（1）连接OD，设OC交BD于K．想办法证明△ODC≌△OBC（SSS）即可解决问题．
（2）由CD=AD，可以假设AD=a，CD=a，设KC=b．由△CDK∽△COD，推出＝，推出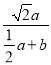＝整理得：2（）2+（）-4=0，解得＝．

（1）证明：连接OD，设OC交BD于K．

∵AB是直径，

∴∠ADB＝90°，

∴AD⊥BD，

∵OC∥AD，

∴OC⊥BD，

∴DK＝KB，

∴CD＝CB，

∵OD＝OB，OC＝OC，CD＝CB，

∴△ODC≌△OBC（SSS），

∴∠ODC＝∠OBC，

∵CB⊥AB，

∴∠OBC＝90°，

∴∠ODC＝90°，

∴OD⊥CD，

∴CD是⊙O的切线．

（2）∵CD＝AD，

∴可以假设AD＝a，CD＝a，设KC＝b．

∵DK＝KB，AO＝OB，

∴OK＝AD＝a，

∵∠DCK＝∠DCO，∠CKD＝∠CDO＝90°，

∴△CDK∽△COD，

∴＝，

∴＝

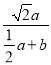整理得：2（）2+（）﹣4＝0，

解得＝或（舍弃），

∵CK∥AD，

∴＝＝＝．