��Ŀ����
����Ŀ�������ͥ��ȼ����Ϊ��ˮ������ȼ�ϣ���Լ�����������ճ������зdz���ʵ������.ij��ȼ������ťλ�ô�0�ȵ�90�ȣ�ȼ���ر�ʱ��ȼ������ťλ��Ϊ0�ȣ���ť�Ƕ�Խ��ȼ������Խ��ȼ���������ʱ����ť�Ƕ�Ϊ90��.Ϊ����ȼ������ť�ڲ�ͬλ���ϵ�ȼ������������ͬ�����£�ѡ����ȼ������ť��5����ͬλ���Ϸֱ��տ�һ��ˮ������ť�Ƕ�̫Сʱ����������ܹ���ˮ�տ�����ѡ����ť�Ƕ�![]() �ȵķ�Χ��
�ȵķ�Χ��![]() ������¼������ݵõ��±���
������¼������ݵõ��±���
��ť�Ƕȣ��ȣ� | 20 | 50 | 70 | 80 | 90 |
����ȼ���������� | 73 | 67 | 83 | 97 | 115 |
��1���������ѧϰ����һ�κ����������������Ͷ��κ�����ȷ�����ֺ����ܱ�ʾ����ȼ����![]() ������ת�Ƕ�
������ת�Ƕ�![]() �ȵı仯���ɣ�˵��ȷ�����ֺ����������������������ɣ���������Ľ���ʽ��
�ȵı仯���ɣ�˵��ȷ�����ֺ����������������������ɣ���������Ľ���ʽ��
��2������ת�Ƕ�Ϊ����ʱ���տ�һ��ˮ����ȼ�������٣������Ƕ��٣�
��3��ij��ͥʹ�ô˿�ȼ�����ǰϰ�߰�ȼ����������ֲ������ʡȼ������ת�Ƕȣ����ü�ͥ����ÿ�µ�ƽ��ȼ������Ϊ13�����ף�������ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ�����������ף�
���𰸡���1��![]() ����2������ת�Ƕ�Ϊ40��ʱ���տ�һ��ˮ����ȼ�������٣�����Ϊ65������3����ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��
����2������ת�Ƕ�Ϊ40��ʱ���տ�һ��ˮ����ȼ�������٣�����Ϊ65������3����ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��![]() ������.
������.
��������
��1���ȼ��躯��Ϊһ�κ�������ѡ���������������ʽ���ٽ����������֤���ټ��躯��Ϊ���κ�������ѡ�������������ʽ���ٽ����������֤��
��2������1��������κ�������ʽ����Ϊ����ʽ��ת��Ϊ���κ�����ֵ�����⣬���ɽ��
��3���ɣ�2��������֪���������ʡȼ������ť�Ƕ�40�ȱȰ�ȼ���������ʱ�տ�һ��ˮ��Լ����115-65-50������ü�ͥ��ǰÿ��ƽ��������Ϊa�����ף��ݴ˽��.
�⣺��1���ټ���仯����Ϊһ�κ���![]() ��
��![]()
����20��73���ͣ�50��67�����뺯������ʽ��
��![]() ���
��� 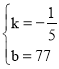
�� ![]() ��
��
��![]() ������ʽ��
������ʽ��
�ɵã�![]()
���Ըñ仯���ɲ���һ�κ���.
���ټ���仯����Ϊ����������![]() ��
��
����20��73�����뺯������ʽ����![]() ��
��
��![]() ��
��
��![]() ������ʽ��
������ʽ��
�ɵ�![]()
���Ըñ仯���ɲ��Ƿ���������.
�ۼ���仯����Ϊ���κ���![]()
����20��73������50��67���ͣ�70��83�����뺯������ʽ��
��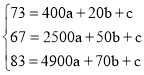 ���
��� 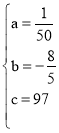
��![]()
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��ö��κ����������е㣬
�ʸñ仯����Ϊ���κ���������ʽΪ��![]() .
.
��2���ɣ�1����֪![]() ��
��
���Ե�![]() ʱ��
ʱ��![]() ֵ��С������СֵΪ65.
ֵ��С������СֵΪ65.
������ת�Ƕ�Ϊ40��ʱ���տ�һ��ˮ����ȼ�������٣�����Ϊ65��.
��3����ü�ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��![]() �����ף�
�����ף�
���ݽ�Լǰ��ı�����ȼ������������Լ�ı�����ȣ�
��![]() ��
��
���![]() �������ף���
�������ף���
���ü�ͥ����ÿ��ƽ���ܱ���ǰÿ�½�ʡȼ��![]() ������.
������.

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�