题目内容
【题目】如图,已知四边形![]() 为
为![]() 的内接四边形,对角线
的内接四边形,对角线![]() 、
、![]() 交于
交于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)作![]() 的角分线
的角分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与
与![]() 交于
交于![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)详见解析;(3)4
【解析】
(1)先判断出∠OBD=∠ODB,再判断出∠OBA=∠ODA,进而得出∠ADB=∠ABD,即可得出结论;
(2)设∠ADF=![]() ,则∠ABF=∠DBF=
,则∠ABF=∠DBF=![]() ,∠ADB=
,∠ADB=![]() ,∠O=
,∠O=![]() ,∠EFD=
,∠EFD=![]() ,∠OFD=
,∠OFD=![]() ,所以∠OFE=
,所以∠OFE=![]() ,结论得证;
,结论得证;
(3)连接DQ,在FQ上取一点N使∠ADN=∠ADF,连接AN,证明△AQN≌△DQN≌△DQE,得出∠EQD=∠DQN=∠AQN=![]() ,求出
,求出![]() =10°,求出BP,BE长,则AD长可求出.
=10°,求出BP,BE长,则AD长可求出.
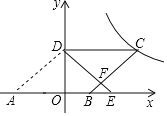
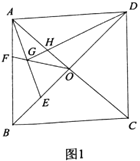
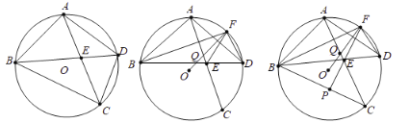
(1)如图1,连接OA、OB、OD,
∴OB=OD,
∴∠OBD=∠ODB,
∵OA=OB=OD,
∴∠OAB=∠OBA,∠OAD=∠ODA,
∵∠ACB=∠ACD,
∴∠AOB=∠AOD,
∴∠OBA=∠ODA,
∴∠ADB=∠ABD,
∴AB=AD;
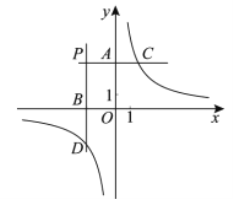
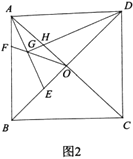
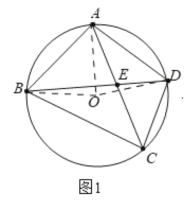
(2)如图2,连接OD,设∠ADF=![]() ,
,
∴∠ABF=∠DBF=![]() ,
,
∴∠ADB=![]() ,∠O=
,∠O=![]() ,
,
∵![]()
∴![]()
∴∠EDF=![]() +
+![]() =
=![]()
∴∠EFD=![]() ,
,
∠OFD=![]() ,
,
∴∠OFE=∠OFD-∠EFD=![]() ,
,
∴∠ADF=2∠OFE;

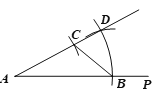
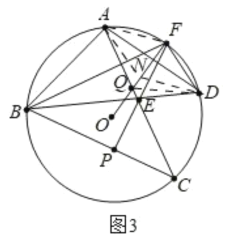
(3)如图3,连接DQ,在FQ上取一点N使∠ADN=∠ADF,连接AN,
∵∠FDE=![]() ,EP⊥BC,
,EP⊥BC,
∴∠BEP=![]() ,∠CBD=∠CAD=
,∠CBD=∠CAD=![]() ,OF垂直平分AD,∠FAD=∠DAN=
,OF垂直平分AD,∠FAD=∠DAN=![]() ,
,
∴∠QAN=![]() ,QA=QD,
,QA=QD,
∴∠NDQ=![]() ,∠BDN=
,∠BDN=![]() ,
,
∴∠EDN=![]() ,DE=DF=DN=AN,AQ=QD,
,DE=DF=DN=AN,AQ=QD,
∴△AQN≌△DQN≌△DQE(SAS),
∴∠EQD=∠DQN=∠AQN=![]() ,
,
∴![]()
∴![]() ,
,
∴∠ABE=![]() ,
,
∴∠BEA=∠BAE=![]() ,AD=AB=BE,
,AD=AB=BE,
在Rt△BPE中,∠PBE=![]() ,
,
∴BP=![]() ,BE=
,BE=![]()
∴AD=4.
故答案为:4

 全能测控期末小状元系列答案
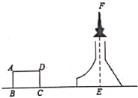
全能测控期末小状元系列答案【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
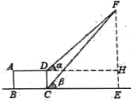
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)