ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯп![]() ЃЈ
ЃЈ![]() ЁЂ
ЁЂ![]() ЮЊГЃЪ§ЃЉЕФЖЅЕуЮЊ
ЮЊГЃЪ§ЃЉЕФЖЅЕуЮЊ![]() ЃЌЕШбќжБНЧШ§НЧаЮ
ЃЌЕШбќжБНЧШ§НЧаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌжБНЧЖЅЕу
ЃЌжБНЧЖЅЕу![]() дкЕкЫФЯѓЯоЃЎ
дкЕкЫФЯѓЯоЃЎ
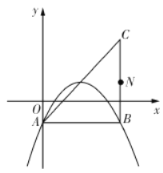
ЃЈ1ЃЉШчЭМЃЌШєИУХзЮяЯпОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧѓИУХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
СНЕуЃЌЧѓИУХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
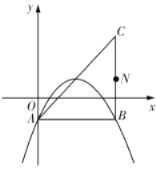
ЃЈ2ЃЉЦНвЦЃЈ1ЃЉжаЕФХзЮяЯпЃЌЪЙЖЅЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЛЌЖЏЃЌЧвгы
ЩЯЛЌЖЏЃЌЧвгы![]() НЛгкСэвЛЕу
НЛгкСэвЛЕу![]() ЃЎ
ЃЎ
ЂйШєЕу![]() дкжБЯп
дкжБЯп![]() ЯТЗНЃЌЧвЮЊЦНвЦЧАЃЈ1ЃЉжаЕФХзЮяЯпЩЯЕФЕуЃЌЕБвд
ЯТЗНЃЌЧвЮЊЦНвЦЧАЃЈ1ЃЉжаЕФХзЮяЯпЩЯЕФЕуЃЌЕБвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕу
Ш§ЕуЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛЂк
ЃЛЂк![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕу![]() ЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЂйЪзЯШЧѓГіжБЯп![]() ЕФНтЮіЪНКЭЯпЖЮ
ЕФНтЮіЪНКЭЯпЖЮ![]() ЕФГЄЖШЃЌзїЮЊКѓајМЦЫуЕФЛљДЁЃЎ
ЕФГЄЖШЃЌзїЮЊКѓајМЦЫуЕФЛљДЁЃЎ
Шє![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌдђПЩЗжЮЊвдЯТСНжжЧщПіЃК
ЮЊЕШбќжБНЧШ§НЧаЮЃЌдђПЩЗжЮЊвдЯТСНжжЧщПіЃК
ЕБ![]() ЮЊжБНЧБпЪБЃКЕу
ЮЊжБНЧБпЪБЃКЕу![]() ЕН
ЕН![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЎДЫЪБЃЌНЋжБЯп
ЃЎДЫЪБЃЌНЋжБЯп![]() ЯђгвЦНвЦ4ИіЕЅЮЛКѓЫљЕУжБЯп
ЯђгвЦНвЦ4ИіЕЅЮЛКѓЫљЕУжБЯп![]() гыХзЮяЯпЕФНЛЕуЃЌМДЮЊЫљЧѓжЎ
гыХзЮяЯпЕФНЛЕуЃЌМДЮЊЫљЧѓжЎ![]() ЕуЃЛ
ЕуЃЛ
ЕБ![]() ЮЊаББпЪБЃКЕу
ЮЊаББпЪБЃКЕу![]() ЕН
ЕН![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЎДЫЪБЃЌНЋжБЯп
ЃЎДЫЪБЃЌНЋжБЯп![]() ЯђгвЦНвЦ2ИіЕЅЮЛКѓЫљЕУжБЯп
ЯђгвЦНвЦ2ИіЕЅЮЛКѓЫљЕУжБЯп![]() гыХзЮяЯпЕФНЛЕуЃЌМДЮЊЫљЧѓжЎ
гыХзЮяЯпЕФНЛЕуЃЌМДЮЊЫљЧѓжЎ![]() ЕуЃЎ
ЕуЃЎ
ЂкгЩЂйПЩжЊЃЌ![]() ЮЊЖЈжЕЃЌвђДЫЕБ
ЮЊЖЈжЕЃЌвђДЫЕБ![]() ШЁзюаЁжЕЪБЃЌ
ШЁзюаЁжЕЪБЃЌ![]() газюДѓжЕЃЎ
газюДѓжЕЃЎ
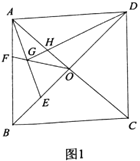
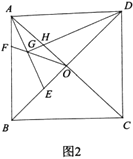
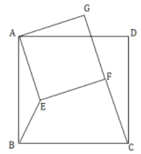
ШчД№ЭМ2ЫљЪОЃЌзїЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌгЩЗжЮіПЩжЊЃЌЕБ
ЃЌгЩЗжЮіПЩжЊЃЌЕБ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() жаЕуЃЉШ§ЕуЙВЯпЪБЃЌ
жаЕуЃЉШ§ЕуЙВЯпЪБЃЌ![]() зюаЁЃЌзюаЁжЕЮЊЯпЖЮ
зюаЁЃЌзюаЁжЕЮЊЯпЖЮ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ
НтЃКЃЈ1ЃЉ![]() ЕШбќжБНЧШ§НЧаЮ
ЕШбќжБНЧШ§НЧаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]()
![]() Еу
Еу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
![]() ХзЮяЯпЙ§
ХзЮяЯпЙ§![]() ЃЌ
ЃЌ![]() СНЕуЃЌ
СНЕуЃЌ
![]()
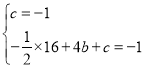 ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃК
ХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃК![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂй![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК![]() ЃЎ
ЃЎ
ЩшЦНвЦЧАХзЮяЯпЕФЖЅЕуЮЊ![]() ЃЌдђгЩЃЈ1ЃЉПЩЕУ
ЃЌдђгЩЃЈ1ЃЉПЩЕУ![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧв
ЃЌЧв![]() дкжБЯп
дкжБЯп![]() ЩЯЃЎ
ЩЯЃЎ
![]() Еу
Еу![]() дкжБЯп
дкжБЯп![]() ЩЯЛЌЖЏЃЌ
ЩЯЛЌЖЏЃЌ
![]() ПЩЩш
ПЩЩш![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
дђЦНвЦКѓХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃК![]() ЃЎ
ЃЎ
НтЗНГЬзщЃК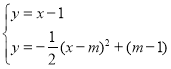 ЃЌ
ЃЌ
НтЕУ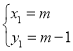 ЃЌ
ЃЌ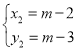
![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Й§Еу![]() зї
зї![]() жсЃЌЙ§Еу
жсЃЌЙ§Еу![]() зї
зї![]() жсЃЌдђ
жсЃЌдђ
![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
Шєвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЮЊЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌдђПЩЗжЮЊвдЯТСНжжЧщПіЃК
Ш§ЕуЮЊЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌдђПЩЗжЮЊвдЯТСНжжЧщПіЃК
ЕБ![]() ЮЊжБНЧБпЪБЃКЕу
ЮЊжБНЧБпЪБЃКЕу![]() ЕН
ЕН![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЈМДЮЊ
ЃЈМДЮЊ![]() ЕФГЄЃЉЃЎ
ЕФГЄЃЉЃЎ
гЩ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ПЩжЊЃЌ
ПЩжЊЃЌ
![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌЧв
ЮЊЕШбќжБНЧШ§НЧаЮЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ШчЭМ1ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЃЌНЛХзЮяЯп
ЃЌНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЮЊЗћКЯЬѕМўЕФЕуЃЎ
ЮЊЗћКЯЬѕМўЕФЕуЃЎ
![]() ПЩЩшжБЯп
ПЩЩшжБЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК![]() ЃЎ
ЃЎ
НтЗНГЬзщ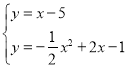 ЃЌ
ЃЌ
ЕУЃК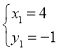 ЃЌ
ЃЌ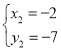
![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЕБ![]() ЮЊаББпЪБЃК
ЮЊаББпЪБЃК![]() ЃЌПЩЧѓЕУЕу
ЃЌПЩЧѓЕУЕу![]() ЕН
ЕН![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЎ
ЃЎ
ШчД№ЭМ2ЃЌШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
гЩ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ПЩжЊЃК
ПЩжЊЃК
![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвЕу
ЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЎ
ЃЎ
Й§Еу![]() зїжБЯп
зїжБЯп![]() ЃЌНЛХзЮяЯп
ЃЌНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЮЊЗћКЯЬѕМўЕФЕуЃЎ
ЮЊЗћКЯЬѕМўЕФЕуЃЎ
![]() ПЩЩшжБЯп
ПЩЩшжБЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК![]() ЃЎ
ЃЎ
НтЗНГЬзщ ЃЌ
ЃЌ
ЕУЃК ЃЌ
ЃЌ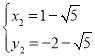
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЫљгаЗћКЯЬѕМўЕФЕу![]() ЕФзјБъЮЊЃК
ЕФзјБъЮЊЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Ђк![]() ДцдкзюДѓжЕЃЎРэгЩШчЯТЃК
ДцдкзюДѓжЕЃЎРэгЩШчЯТЃК
гЩЂйжЊ![]() ЮЊЖЈжЕЃЌдђЕБ
ЮЊЖЈжЕЃЌдђЕБ![]() ШЁзюаЁжЕЪБЃЌ
ШЁзюаЁжЕЪБЃЌ![]() газюДѓжЕЃЎ
газюДѓжЕЃЎ
ШчД№ЭМ2ЃЌШЁЕу![]() Йигк
Йигк![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌвзЕУЕу
ЃЌвзЕУЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
СЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
взЕУ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
![]() ЫФБпаЮ
ЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЎ
ЮЊЦНааЫФБпаЮЃЎ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
![]() ЕБ
ЕБ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЙВЯпЪБЃЌ
Ш§ЕуЙВЯпЪБЃЌ![]() зюаЁЃЌзюаЁжЕЮЊ
зюаЁЃЌзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
![]()
![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ

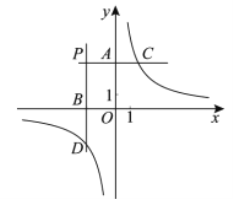
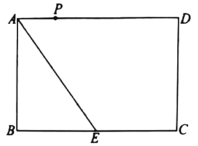
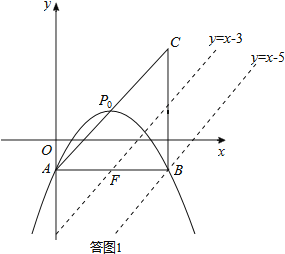
ЁОЬтФПЁПШчЭМ1ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧжЃжнЪаЖўЦпЧјШ§ИіРЌЛјДцЗХЕуЃЌЕу
ЪЧжЃжнЪаЖўЦпЧјШ§ИіРЌЛјДцЗХЕуЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЛгкЕу
ЗжБ№ЮЛгкЕу![]() ЕФе§ББКЭе§ЖЋЗНЯђЃЌ
ЕФе§ББКЭе§ЖЋЗНЯђЃЌ![]() УзЃЎАЫЮЛЛЗЮРЙЄШЫЗжБ№ВтЕУЕФ
УзЃЎАЫЮЛЛЗЮРЙЄШЫЗжБ№ВтЕУЕФ![]() ГЄЖШШчЯТБэЃК
ГЄЖШШчЯТБэЃК
Мз | ЖЁ | Бћ | ЖЁ | Юь | ач | Щъ | ГН | |
| 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
ЫћУЧгжЕїВщСЫИїЕуЕФРЌЛјСПЃЌВЂЛцжЦСЫЯТСаМфВЛЭъећЕФЭГМЦЭМ2ЃЎ
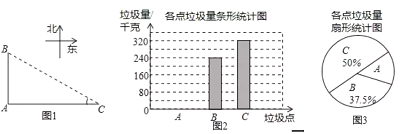
ЃЈ1ЃЉБэжаЕФжаЮЛЪ§ЪЧ ЁЂжкЪ§ЪЧ ЃЛ
ЃЈ2ЃЉЧѓБэжа![]() ГЄЖШЕФЦНОљЪ§
ГЄЖШЕФЦНОљЪ§![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЧѓ![]() ДІЕФРЌЛјСПЃЌВЂНЋЭМ2ВЙГфЭъећЃЛ
ДІЕФРЌЛјСПЃЌВЂНЋЭМ2ВЙГфЭъећЃЛ
ЃЈ4ЃЉгУЃЈ2ЃЉжаЕФ![]() зїЮЊ
зїЮЊ![]() ЕФГЄЖШЃЌвЊНЋ
ЕФГЄЖШЃЌвЊНЋ![]() ДІЕФРЌЛјбиЕРТЗ
ДІЕФРЌЛјбиЕРТЗ![]() ЖМдЫЕН
ЖМдЫЕН![]() ДІЃЌвбжЊдЫЫЭ1ЧЇПЫРЌЛјУПУзЕФЗбгУЮЊ0.005дЊЃЌЧѓдЫРЌЛјЫљашЕФЗбгУЃЎ
ДІЃЌвбжЊдЫЫЭ1ЧЇПЫРЌЛјУПУзЕФЗбгУЮЊ0.005дЊЃЌЧѓдЫРЌЛјЫљашЕФЗбгУЃЎ