题目内容
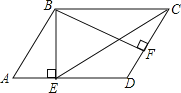
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
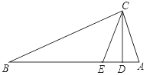
【答案】(1)证明见解析;(2)8.
【解析】
(1)依据∠ACB=90°,CD⊥AB,即可得到∠ACD=∠B,再根据CE平分∠BCD,可得∠BCE=∠DCE,进而得出∠AEC=∠ACE;
(2)依据∠ACD=∠BCE=∠DCE,∠ACB=90°,即可得到∠ACD=30°,进而得出Rt△ACD中,AC=2AD=4,Rt△ABC中,AB=2AC=8.
解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴在Rt△ACD中,AC=2AD=4,
∴在Rt△ABC中,AB=2AC=8.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成如下图所示统计图:
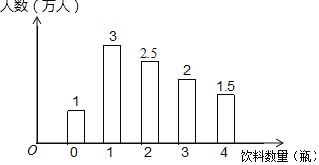
(1)在A出口的被调查游客中,购买瓶装饮料的数量的中位数是______瓶、众数是______瓶、平均数是______瓶;
(2)已知A、B、C三个出口的游客量比为2:2:1,用上面图表的人均购买饮料数量计算:这一天景区内若有50万游客,那么这一天购买的饮料的总数是多少?
表一:
出口 | B | C |
人均购买饮料数量(瓶) | 3 | 2 |
(3)若每瓶饮料要消耗0.5元处理包装的环保费用,该日需要花费多少钱处理这些饮料瓶?由此请你对游客做一点环保宣传建议.