Question

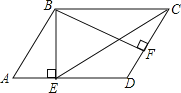
【题目】在平行四边形ABCD中，BE⊥AD于点E，BF⊥CD于点F，若∠EBF=60°，且AE=2，DF=1，则EC的长为_____________.

Answer 1

【答案】4

【解析】

由平行四边形的性质和已知条件得出∠ABE=∠CBF=30°，得出CD=AB=2AE=4，由勾股定理求出BE，得出BC=2CF=6，再根据勾股定理即可求出EC．

∵四边形ABCD是平行四边形，

∴AB∥CD，BC∥AD，AB=CD，

∵BE⊥AD，BF⊥CD，

∴BE⊥BC，BF⊥AB，

∴∠ABF=∠EBC=90°，

∵∠EBF=60°，

∴∠ABE=∠CBF=30°，

∵AE=2，DF=1，

∴CD=AB=2AE=4，

∴BE=，CF=4-1=3，

∴BC=2CF=6，

∴EC=；

故答案为：4．