题目内容
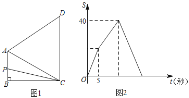
【题目】如图1，四边形ABCD中，AB∥CD，∠B=90°，AC=AD．动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动，在整个运动过程中，△BCP的面积S与运动时间t（秒）的函数图象如图2所示，则AD等于（ ）
A. 10B. 
C. 8D. 
【答案】B
【解析】
当t=5时，点P到达A处，根据图象可知AB=5；当s=40时，点P到达点D处，根据三角形BCD的面积可求出BC的长，再利用勾股定理即可求解．
解：当t=5时，点P到达A处，根据图象可知AB=5，
过点A作AE⊥CD交CD于点E，则四边形ABCE为矩形，
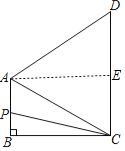
∵AC=AD，
∴DE=CE=
CD，
当s=40时，点P到达点D处，
则S=CDBC=（2AB）BC=5×BC=40，
∴BC=8，
∴AD=AC=
.
故选：B．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
