题目内容
 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是
- A.

- B.

- C.
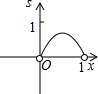
- D.

B
分析:根据条件正方形中AE=BF=CG=DH可知△AEH≌△BFE≌△CGF≌△DHG,设AE为x,则AH=1-x,根据勾股定理EH2=AE2+AH2=x2+(1-x)2,进而可求出函数解析式,求出答案.
解答:∵根据正方形的四边相等,四个角都是直角,且AE=BF=CG=DH,
∴可证△AEH≌△BFE≌△CGF≌△DHG.
设AE为x,则AH=1-x,根据勾股定理,得
EH2=AE2+AH2=x2+(1-x)2
即s=x2+(1-x)2.
s=2x2-2x+1,
∴所求函数是一个开口向上,对称轴是x= .
.
∴自变量的取值范围是大于0小于1.
故选B.
点评:本题考查了动点问题的函数图象,解题时需根据自变量的取值范围,并且可以考虑求出函数的解析式来解决.
分析:根据条件正方形中AE=BF=CG=DH可知△AEH≌△BFE≌△CGF≌△DHG,设AE为x,则AH=1-x,根据勾股定理EH2=AE2+AH2=x2+(1-x)2,进而可求出函数解析式,求出答案.
解答:∵根据正方形的四边相等,四个角都是直角,且AE=BF=CG=DH,
∴可证△AEH≌△BFE≌△CGF≌△DHG.
设AE为x,则AH=1-x,根据勾股定理,得
EH2=AE2+AH2=x2+(1-x)2
即s=x2+(1-x)2.
s=2x2-2x+1,
∴所求函数是一个开口向上,对称轴是x=
 .
.∴自变量的取值范围是大于0小于1.
故选B.
点评:本题考查了动点问题的函数图象,解题时需根据自变量的取值范围,并且可以考虑求出函数的解析式来解决.

练习册系列答案
相关题目
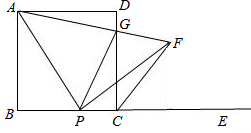 AP,与∠DCE的平分线CF,相交于点F,连接AF,与边CD相交于点G,连接PG.
AP,与∠DCE的平分线CF,相交于点F,连接AF,与边CD相交于点G,连接PG. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. (2013•桂林模拟)如图,已知,正方形ABCD的边长为1,以BC为对角线作第一个正方形BECO1,再以BE边为对角线作第二个正方形EFBO2,如此作下去,…则所作的第n正方形的面积Sn=
(2013•桂林模拟)如图,已知,正方形ABCD的边长为1,以BC为对角线作第一个正方形BECO1,再以BE边为对角线作第二个正方形EFBO2,如此作下去,…则所作的第n正方形的面积Sn=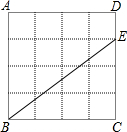 (2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.
(2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.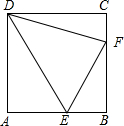 (2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.
(2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.