题目内容
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
【答案】(1)3;(2)![]() ;(3)n>0
;(3)n>0
【解析】
(1)观察已知表格中的对应值可知:该函数图象的开口向上,对称轴是直线x=1,由抛物线的对称性可知:x=3时的对应函数值与x= -1时的对应函数值相等,即可求得![]() 的值;
的值;
(2)把表中的三个点![]() 、(1,-1)、(2, 0)代入函数的解析式,得到关于a,b,c的方程组,即可求得解析式;
、(1,-1)、(2, 0)代入函数的解析式,得到关于a,b,c的方程组,即可求得解析式;
(3)根据函数的图象开口方向,增减性即可确定.
(1)观察已知表格中的对应值可知:该函数图象的开口向上,对称轴是直线x=1,
∴由抛物线的对称性可知:x=3时的对应函数值与x= -1时的对应函数值相等,即m的值为3;
(2)把![]() 、(1,-1)、(2, 0)代入二次函数
、(1,-1)、(2, 0)代入二次函数![]()
![]() ,得
,得
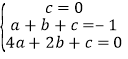 ,
,
解得: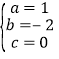
∴这个二次函数的解析式为![]() ;
;
(3)∵该函数图象的开口向上,对称轴是直线x=1,
∴若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,则
点A(n+2,y1),B(n,y2)在对称轴两侧时,n+2-1![]() 1-n且
1-n且![]() ,
,
解得:![]() ;
;
点A(n+2,y1),B(n,y2)在对称轴同侧(含顶点)时,![]() ,
,
综上可知:n的取值范围是n![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.