题目内容
【题目】欧尚超市准备代销一款运动鞋,每双的成本是160元,为了合理定价,投放市场进行试销.据市场调查,销售单价是200元时,每天的销售量是40双,而销售单价每降低1元,每天就可多售出6双(售价不得低于160元/双),设每双降低售价x元(x为正整数),每天的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每双运动鞋的售价定为多少元时,每天可获得最大利润?最大利润是多少?
【答案】(1)y=6x2+200x+1600,1≤x≤40,且x为正整数;(2)每双运动鞋售价定为183元时,该款运动鞋每天可获得最大利润为3266元.
【解析】
(1)根据“利润=(售价-成本)×销售量”列出y与x的函数关系式,即可;
(2)把(1)中的二次函数解析式转化为顶点式,利用二次函数图象和性质,进行解答.
(1)根据题意可得:y=(200x160)(40+6x)=6x2+200x+1600,
x的取值范围为:1≤x≤40,且x为正整数;
(2)∵y=6x2+200x+1600=6(x![]() )2+
)2+![]() , 1≤x≤40,且x为正整数;
, 1≤x≤40,且x为正整数;
∴当x=17,即售价定为每双183元时,y有最大值,最大值为3266元,
答:每双运动鞋售价定为183元时,该款运动鞋每天可获得最大利润为3266元.

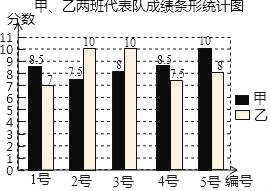
【题目】甲、乙两班分别选5名同学组成代表队参加学校组织的“国防知识”选拔赛,现根据成绩(满分10分)制作如图统计图和统计表(尚未完成)
甲、乙两班代表队成绩统计表
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | a | 0.7 |
乙班 | 8.5 | b | 10 | 1.6 |
请根据有关信息解决下列问题:
(1)填空:a= ,b= ;
(2)学校预估如果平均分能达8.5分,在参加市团体比赛中即可以获奖,现应选派 代表队参加市比赛;(填“甲”或“乙”)
(3)现将从成绩满分的3个学生中随机抽取2人参加市国防知识个人竞赛,请用树状图或列表法求出恰好抽到甲,乙班各一个学生的概率.