جâؤ؟ؤعبف
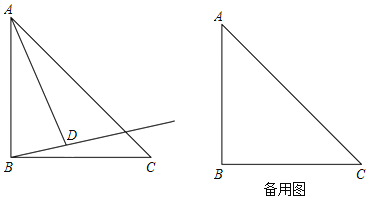
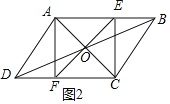
،¾جâؤ؟،؟ABCDضذ£¬¶ش½ادكAC،¢BDدཻسعµمO£¬Eتا±كABةدµؤز»¸ِ¶¯µم£¨²»سëA،¢Bضط؛د£©£¬ء¬½سEO²¢رس³¤£¬½»CDسعµمF£¬ء¬½سAF£¬CE£¬دآءذثؤ¸ِ½لآغضذ£؛
¢ظ¶شسع¶¯µمE£¬ثؤ±كذخAECFت¼ضصتائ½ذذثؤ±كذخ£»
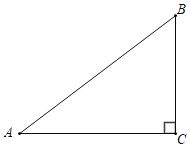
¢عبô،دABC£¼90،م£¬شٍضءةظ´وشعز»¸ِµمE£¬ت¹µأثؤ±كذخAECFتا¾طذخ£»
¢غبôAB£¾AD£¬شٍضءةظ´وشعز»¸ِµمE£¬ت¹µأثؤ±كذخAECFتاءâذخ£»
¢ـبô،دBAC£½45،م£¬شٍضءةظ´وشعز»¸ِµمE£¬ت¹µأثؤ±كذخAECFتاص·½ذخ£®
زشةدثùسذصب·ثµ·¨µؤذٍ؛إتا_____£®
،¾´ً°¸،؟¢ظ¢غ¢ـ
،¾½âخِ،؟
¢ظ¸ù¾فئ½ذذثؤ±كذخµؤذشضتµأAB،خDC£¬OA£½OC£¬شظسةئ½ذذدكµؤذشضت؛ح¶ش¶¥½ادàµب؟ةµأ،دOAE£½،دOCF£¬،دAOE£½،دCOF£¬¸ù¾فASAہ´إذ¶¨،÷AOE،ص،÷COF£¬حئ³ِAE=CF,سة´ث؟ةإذ¶دثؤ±كذخخھئ½ذذثؤ±كذخ£»
¢ع¸ù¾ف¾طذخµؤإذ¶¨¶¨ہي؟ةضھ£¬µ±CE،حABت±£¬ثؤ±كذخAECFخھ¾طذخ£¬¶ّح¼2-2ضذ£¬AB<ADت±£¬µمE²»شعدك¶خABةد£»
¢غ¸ù¾فءâذخµؤإذ¶¨¶¨ہي؟ةضھ£؛µ±EF،حACت±£¬ثؤ±كذخAECFخھءâذخ£»
¢ـµ±CE،حABاز،دBAC£½45،مت±£¬ثؤ±كذخAECFخھص·½ذخ£¬شعABةدز»¶¨´وشعز»µمE
½â£؛£¨1£©بçح¼1£¬
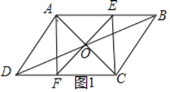
،كثؤ±كذخABCDخھئ½ذذثؤ±كذخ£¬¶ش½ادكACسëBD½»سعµمO£¬
،àAB،خDC£¬AB£½DC£¬OA£½OC£¬OB£½OD£¬
،à،دOAE£½،دOCF£¬
،ك،دAOE£½،دCOF£¬
،à،÷AOE،ص،÷COF£¨ASA£©£¬
،àAE£½CF£¬
سض،كAE،خCF£¬
،àثؤ±كذخAECFخھئ½ذذثؤ±كذخ£¬
¼´EشعABةدبخزâخ»ضأ£¨²»سëA،¢Bضط؛د£©ت±£¬ثؤ±كذخAECF؛مخھئ½ذذثؤ±كذخ£¬
¹تر،دî¢ظصب·£»
£¨2£©بçح¼2£¬µ±،دABC£¼90،م,
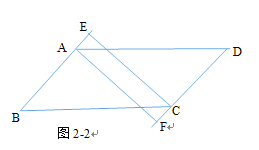
µ±CE،حABت±£¬ثؤ±كذخAECFخھ¾طذخ£¬
شعح¼2ضذ£¬AB>ADت±£¬´وشعز»µمE, ت¹µأثؤ±كذخAECFتا¾طذخ£»
¶ّح¼2-2ضذ£¬AB<ADت±£¬µمE²»شعدك¶خABةد£»
¹تر،دî¢ع²»صب·£®
£¨3£©بçح¼3£¬

µ±EF،حACت±£¬ثؤ±كذخAECFخھءâذخ£¬
،كAB£¾AD£¬
،àشعABةدز»¶¨´وشعز»µمE, ت¹µأثؤ±كذخAECFتا¾طذخ£»
¹تر،دî¢غصب·£®
£¨4£©بçح¼4£¬

µ±CE،حABاز،دBAC£½45،مت±£¬ثؤ±كذخAECFخھص·½ذخ£¬¹تر،دî¢ـصب·£®
¹ت´ً°¸خھ£؛¢ظ¢غ¢ـ£®