题目内容
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
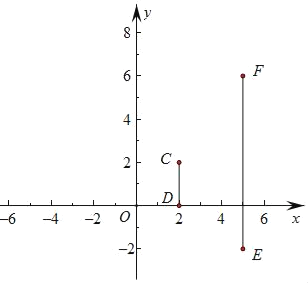
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
【答案】(1)顶点坐标为(3,1);(2)m=﹣![]() ;(3)m<﹣1或m>
;(3)m<﹣1或m>![]() .
.
【解析】
(1)利用配方法得y═m(x﹣3)2+1,由此即可得出顶点坐标;
(2)根据抛物线的对称轴以及AB=4,即可得到A、B两点的坐标,代入抛物线即可求出m的值;
(3)结合图象即可得出当抛物线与线段CD和线段EF都没有公共点时m的取值范围.
(1)∵y=mx2﹣6mx+9m+1=m(x﹣3)2+1,
∴抛物线的顶点坐标为(3,1);
(2)∵对称轴为直线x=3,且AB=4,
∴A(1,0),B(5,0),
将点A的坐标代入抛物线,可得:m=﹣![]() ;
;
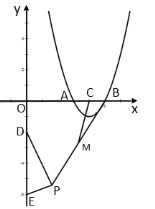
(3)如图:
①当m>0时满足![]() ,解得:m>
,解得:m>![]() ;
;
②当m<时满足![]() ,解得:m<﹣1;
,解得:m<﹣1;
综上,m<﹣1或m>![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制成如下统计图表(单位:cm):
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
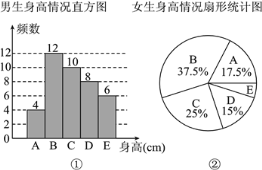
根据图表提供的信息,样本中,身高在160≤x<170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16