题目内容
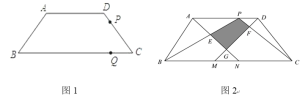
【题目】如图,在正方形ABCD中,以BC为直径作半圆O,以点D为圆心、DA为半径做圆弧交半圆O于点P.连结DP并延长交AB于点E.
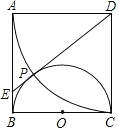
(1)求证:DE为半圆O的切线;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据SSS证得△ODP≌△ODC,从而证得∠OPD=∠OCD=90°,即可证得结论;
(2)根据切线长定理和相似三角形的判定与性质得到:(AB﹣EB)2=EB(2AB+EB),整理得到AB=4EB,即可证得AE=3EB,从而求得![]()
(1)证明:连接OP,OD,
∵BC是⊙O的直径,
∴OP=OC,
∵以点D为圆心、DA为半径做圆弧,
∴PD=CD,
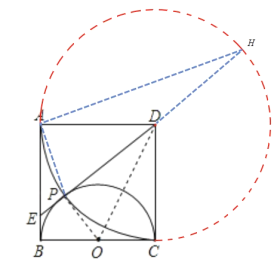
在△ODP和△ODC中,
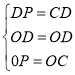 ,
,
∴△ODP≌△ODC(SSS),
∴∠OPD=∠OCD=90°,
∵P点在⊙O上,
∴DE为半圆O的切线;
(2)解:∵以点D为圆心、DA为半径做圆,延长ED与圆的另一个交点为H,连接AP,
四边形ABCD是正方形,
∴EA是⊙D的切线,
![]()
![]()
![]() 为圆D的直径,
为圆D的直径,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴EA2=EPEH,
同理,EB是半圆O的切线,
∵DE为半圆O的切线,
∴EB=EP,
∵AD=PD=AB,
∴(AB﹣EB)2=EP(PH+EP)
∴(AB﹣EB)2=EB(2AB+EB)
整理得AB=4EB,
∴AE=3EB,
∴![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
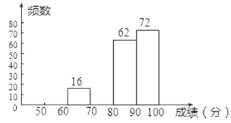
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.