题目内容
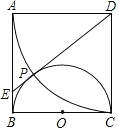
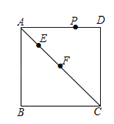
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 、
、![]() 是对角线
是对角线![]() 上的两个动点(点
上的两个动点(点![]() 靠近点
靠近点![]() ),且
),且![]() ,
,![]() 是正方形四边上的任意一点.若
是正方形四边上的任意一点.若![]() 是等边三角形,则 AE的长为______ .
是等边三角形,则 AE的长为______ .
【答案】![]() 或
或![]()
【解析】
当点P在AD上时,过点PH⊥EF于H,由等边三角形的性质可求PH=![]() ,由正方形的性质可求∠DAC=45°,AC=
,由正方形的性质可求∠DAC=45°,AC=![]() ,可得AH=PH,可求AE=
,可得AH=PH,可求AE=![]() ,,同理可求点P在AB,CD,BC上时,AE的值,即可求解.
,,同理可求点P在AB,CD,BC上时,AE的值,即可求解.
如图,当点P在AD上,且点E在点F上方时,过点PH⊥EF于H,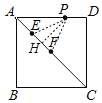
∵△PEF是等边三角形,PH⊥EF,
∴∠PEF=60°,PE=PF=EF=2,EH=FH=1,
∴PH=![]() ,
,
∵四边形ABCD是正方形,AB=4,
∴∠DAC=45°,AC=![]() ,
,
∵PH⊥AC,
∴∠APH=∠PAH=45°,
∴AH=PH=![]() ,
,
∴AE=![]() ,
,
同理可得:当点P在AB上时,AE=![]() ,
,
同理可得:当点P在CD或BC上时,AE=![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】疫情期间某校学生积极观看网络直播课程,为了了解全校500名学生观看网络直播课程的情况,随机抽取50名学生,对他们观看网络直播课程的节数进行收集,并对数据进行了整理、描述和分析,下面给出了部分信息.
观看直播课节数的频数分布表
节数x | 频数 | 频率 |
| 8 | 0.16 |
| 10 | 0.20 |
| 16 |
|
|
| 0.24 |
| 4 | 0.08 |
总数 | 50 | 1 |

其中,节数在![]() 这一组的数据是:
这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() __________,
__________,![]() __________
__________
(2)请补全频数分布直方图;
(3)随机抽取的50名学生观看直播课节数的中位数是___________;
(4)请估计该校学生中观看网络直播课节数不低于30次的约有__________人.