题目内容
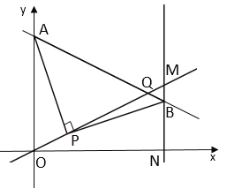
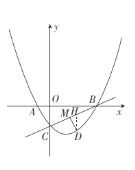
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 二次函数
二次函数![]() 的图象经过
的图象经过![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
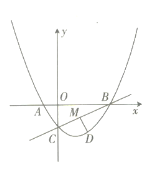
![]() 求二次函数的解析式及点
求二次函数的解析式及点![]() 的坐标.
的坐标.
![]() 点
点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上.设点
下方的二次函数图象上.设点![]() 的横坐标为
的横坐标为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 求线段
求线段![]() 的长关于
的长关于![]() 的函数解析式,并求线段
的函数解析式,并求线段![]() 的最大值.
的最大值.
【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]()
![]() ,
,![]() 有最大值
有最大值![]()
【解析】
(1)根据一次函数的解析式,可得B,C的坐标,由待定系数法,可求得二次函数的解析式;
(2)过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,由D,H的坐标特征,可设
,由D,H的坐标特征,可设![]() ,
,![]() ,易得BOC~DMH,从而得
,易得BOC~DMH,从而得![]() ,进而即可得到结论.
,进而即可得到结论.
(1)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴令y=0,得![]() ,解得:x=4,令x=0,得:y=-2,
,解得:x=4,令x=0,得:y=-2,
∴点![]() 的坐标分别为
的坐标分别为![]() .
.
将点![]() 的坐标代入二次函数的解析式得:
的坐标代入二次函数的解析式得:![]() ,解得:
,解得: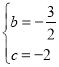 ,
,
∴二次函数的解析式为:![]() ,
,
当![]() 时,
时,![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
(2)过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,
,
∵OB=4,OC=2,
∴BC=![]() ,
,
∵点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上,
下方的二次函数图象上,
∴点![]() ,点
,点![]() (0<m<4),
(0<m<4),
∵DH∥y轴,
∴∠OCB=∠MHD,
∵∠OCB+∠OBC=∠MHD+∠MDH=90°,
∴![]() ,
,
∵∠BOC=∠DMH=90°,
∴BOC~DMH,
∴![]() ,
,
![]()
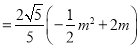
![]() ,(0<m<4),
,(0<m<4),
![]() ,
,
∴当m=2时,![]() 的最大值=
的最大值=![]() .
.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目