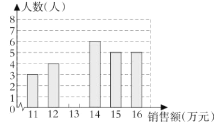
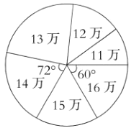
题目内容
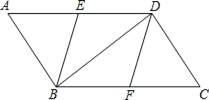
【题目】如图,在矩形ABCD中,点E,F在对角线BD上,BE=DF.请你判断:AE与CF的关系,并加以证明
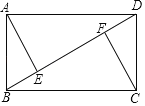
【答案】AE与CF相等且平行;或相等且共线.理由详见解析
【解析】
AE与CF的关系分为数量关系和位置关系两种情况.由平行四边形的性质得出AD=CD,∠ABE=∠CDF,结合BE=DF可证明△ABE≌△CDF,根据全等三角形的性质可得出结论.
解:AE与CF相等且平行;或相等且共线.理由如下:
(1)数量关系:AE=CF.
∵四边形ABCD是矩形,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,
 ,
,
∴△ABE≌△CDF(SAS).
∴AE=CF.
(2)当点E与点F不在BD的中点时,AE∥FC.
∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AED=∠CFB,
∴AE∥CF.
(3)当点E和点F在BD的中点时,AE与CF共线.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目